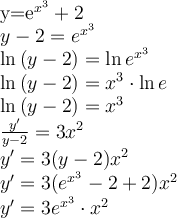
1)10 (км/час) - скорость на велосипеде.
2)8 (см) - длина основания;
10 (см) - длина боковой стороны.
Объяснение:
1. Турист преодолел расстояние в 29 км. 2 часа он ехал на велосипеде,
затем 3 часа шёл пешком. Скорость на велосипеде больше скорости
пешком на 7 км. Найти скорость движения на велосипеде.
х - скорость пешком
х+7 - скорость на велосипеде
3*х - путь пешком
(х+7)*2 - путь на велосипеде
По условию задачи весь путь 29 км, уравнение:
3х+2(х+7)=29
3х+2х+14=29
5х=29-14
5х=15
х=15/5
х=3 (км/час) - скорость пешком
3+7=10 (км/час) - скорость на велосипеде.
2 Периметр равнобедренного треугольника 28 см. Боковая сторона
на 2 см больше основания . Найти стороны РАВНОБЕДРЕННОГО
треугольника.
х - длина основания
х+2 - длина боковой стороны
Периметр треугольника - это сумма длин всех сторон треугольника. Так как треугольник равнобедренный, в нём боковые стороны равны.
По условию задачи периметр треугольника 28 см, уравнение:
х+2(х+2)=28
х+2х+4=28
3х=28-4
3х=24
х=24/3
х=8 (см) - длина основания
8+2=10 (см) - длина боковой стороны.
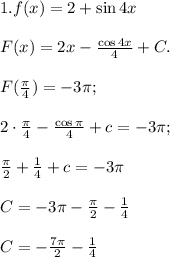
Заданная первообразная - 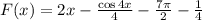
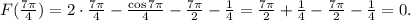
ОТВЕТ: 0.
![2. f(x)=e^x+2x+1, \max_{[0;2]}F(x)=e^2.\\\\F(x)=e^x+x^2+x+C.](/tpl/images/1075/3849/89ce2.png)
График данной первообразная вне зависимости от значения константы на заданном отрезке монотонно возрастает. Поэтому максимальное значение первообразная принимает на правом конце отрезка [0; 2] - т.е. при х = 2.
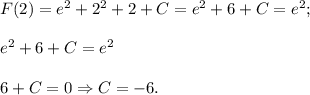
Заданная первообразная - 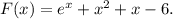
Соответственно все из того же факта монотонного возрастания следует и то, что минимальное значение первообразная принимает на левом конце отрезка [0; 2] - т.е. при х = 0.
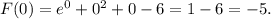
ОТВЕТ: -5.
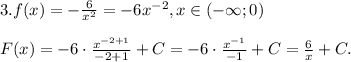
По условию 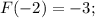
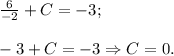
Заданная первообразная - 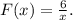
Решим уравнение 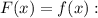
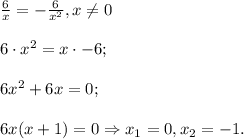
Однако вспоминаем про ограничение для самой переменной: 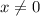 (о чем прописано также и в условии существования первообразной). Делаем вывод: уравнение имеет единственное решение
(о чем прописано также и в условии существования первообразной). Делаем вывод: уравнение имеет единственное решение 
ОТВЕТ: {-1}.