а)

ОДЗ:у-любое число
б)

ОДЗ:у-любое число,кроме у≠9
у-9=0
у=9
в)

ОДЗ:у-любое число, кроме у≠3,у≠ -3
у²-9=0
(у-3)(у+3)=0
у-3=0 или у+3=0
у=3 у= -3
г)

ОДЗ:у-любое число
у²+3=0
у²≠ -3
ответ:уравнение не существует, квадрат числа не может быть отрицательным
д)
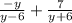
ОДЗ:у-любое число,кроме у≠6,у≠ -6
у-6=0 или у+6=0
у=6 у= -6
е)
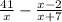
ОДЗ-х-любое число,кроме х≠0,х≠ -7
х=0 или х+7=0
х= -7
II варианта)
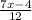
ОДЗ:х-любое число
б)
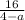
ОДЗ:а-любое число,кроме а≠4
4-а=0
-а= -4
а=4
в)
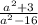
ОДЗ:а-любое число, кроме а≠4,а≠ -4
а²-16=0
(а-4)(а+4)=0
а-4=0 или а+4=0
а=4 а= -4
г)
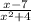
ОДЗ:х-любое число
х²+4=0
х²≠ -4
ответ:уравнение не существует, квадрат числа не может быть отрицательным
д)

ОДЗ:х-любое число,кроме х≠4,х≠ -4
х-4=0 или х+4=0
х=4 х= -4
е)
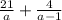
ОДЗ:а-любое число,кроме а≠0,а≠1
а=0 или а-1=0
а=1
ОДЗ-область допустимых значений1)
a)x^8+x^4-2=(x^4+2)(x^4-1)=(x^4+2)(x-1)(x+1)(x^2+1)
b)a^5-a^2-a-1=a(a^4-1)-(a^2+1)=a(a^2-1)(a^2+1)-(a^2+1)=(a^2+1)(a^3-a-1)
2)
пусть натуральное число-а,тогда
(а^2-1)=(а-1)(а+1)
так как А не делится на 3,то всегда либо А-1,либо А+1 будет делится на три.
3)рассмотрим произведение первых двух скобок:
(2+1)(2^2+1)=2^3+2^2+2+1,домножим на третью скобку
(2^3+2^2+2+1)(2^4+1)=2^7+2^6+2^5+2^3+2^2+2^1
Заметим закономерность:произведение n скобок дает нам сумму степеней двойки,начиная с (2n-1)
то есть,для произведения всех наших скобок,их 6,справедливо равенство:2^63+2^62+2^61+...+2^2+2+1=2^64-1
4)натуральными называются целые неотрицательные числа=>
мы можем сделать ограничения на х и на у:
1<=x<=7 и 1<=y<=3
Потому что если х и у не будут в этих промежутках,тогда сумма превысит 23
Таким образом нам надо перебрать три варианта:
у=1=>х=16/3 не натуральное-не подходит
у=2=>x=3-подходит
у=3=>х=2/3 не натуральное-не подходит
ответ (3;2)
x г/см^3 - 2600 кг/м^3
x = 2600/1000 = 2,6 г/см^3