1) Обозначим первую цифру задуманного числа х, а вторую - у. Выполнив указанные действия, получим:
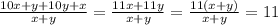
Т.е., всегда будет получаться 11.
2) Признак делимости на 3: на три делятся те числа, сумма цифр которых делится на 3.
Данное число (10^n+317) будет состоять из единицы, n нулей, тройки, единицы и семёрки. Сумма цифр равна 1+3+1+7 = 12.
12 делится на 3, значит, и число 10^n+317 тоже делится на 3, ЧТД
Аналогично, признак делимости на 9: на 9 делятся те числа, сумма цифр которых делится на 9.
10^n состоит из единицы и n нулей. Если от него отнять 1, оно будет состоять из девяток. Соответсвенно, сумма цифр этого числа поделится на 9, ЧТД.
y = √[(4x - 8)/(x² + 2x - 15)]
Воспользуемся методом интервалов
(4x - 8)/(x² + 2x - 15) ≥ 0
4x - 8 = 0
x₁ = 2
x² + 2x - 15 = 0
x₂ = 3 ; x₃ = - 5
- + - +
>
-∞ - 5 2 3 +∞ x
x ∈ (- 5;2] ∪ (3;+ ∞)
.