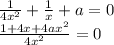
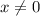и перейдем к следующему уравнению: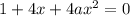
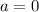, то получим линейное уравнение: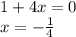
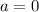удовлетворяет заданному условию.
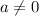, то получаем квадратное уравнение, наличие решений у которого зависит от дискриминанта: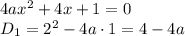
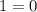, значит остается единственный вариант: приравнять дискриминант к нулю и проверить, будет ли уравнение в этом случае иметь единственный корень: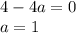
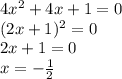
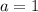также удовлетворяет заданному условию.
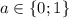, тогда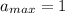 
y'=(x²-9x+9)eˣ +(2x-9)eˣ = (x²-9x+9+2x-9x)eˣ = (x²-7x)eˣ
(x²-7x)eˣ = 0
x(x-7)eˣ = 0
x = 0 или x-7 = 0 или eˣ = 0
х = 7 нет решений
х = 7 не принадлежит заданному отрезку
х = 0 - точка максимума
Проверим ее и границы
у(0) =(0²-9*0+9)e^0 = 9*1 = 9
у(-5) = ((-5)²-9(-5)+9)e^(-5) = (25+45+9)e^(-5) = 79e^(-5)
у(3) = (3²-9*3+9)e^3 = -9e^3
ответ: 79e^(-5)