Дано: bn – геометрическая прогрессия;
b1 + b2 = 30, b2 + b3 = 20;
Найти: b1; b2; b3 - ?
Формула члена геометрической прогрессии: bn = b1 * q^(n – 1),
где b1 – первый член геометрической прогрессии, q – её знаменатель, n – количество членов прогрессии этой формулы выразим второй и третий члены заданной прогрессии:
b2 = b1 * q^(2 – 1) = b1 * q;
b3 = b1 * q^(3 – 1) = b1 * q^2.
Т.о. имеем:
b1 + b2 = 30; и b2 + b3 = 20;
b1 + b1 * q = 30; b1 * q + b1 * q^2 = 20;
b1 (1 + q) = 30; b1 (q + q^2) = 20;
b1 = 30 / (1 + q). b1 = 20 / (q + q^2).
Т.е. 30 / (1 + q) = 20 / (q + q^2);
30 * (q + q^2) = 20 * (1 + q);
30q + 30q^2 = 20 + 20q;
30q^2 + 10q – 20 = 0;
D = (10)^2 – 4 * 30 * (-20) = 2500; sqrt(D) = sqrt (2500) = 50;
q1 = (-10 + 50) / 60 = 2/3;
q2 = (-10 - 50) / 60 = -1.
Подставим оба полученных значений q выражение для нахождения b1:
b1 = 30 / (1 + 2/3) = 30 / (5/3) = 90/5 = 18;
b1 = 30 / (1 + (-1)) = 30 / 0 – смысла не имеет, следовательно, q = 2/3.
b2 = b1 * q = 18 * 2/3 = 12;
b3 = b1 * q^2 = 18 * 2/3^2 = 8.
ответ: b1 = 18; b2 = 12; b3 =8.
Объяснение:
Функция задана формулой f(x) = 2x² - 5x + 3
a)Найдите f(-1)
f(-1) = 2 * (-1)² - 5 * (-1) + 3 = 2 * 1 + 5 + 3 = 2 + 8 = 10
ответ: 10
б) Определите, при каких значениях X выполняется равенство f(x)=1
f(x)=1
2x² - 5x + 3 = 1
2x² - 5x + 2 = 0
D = b² - 4ac = 25 - 4 * 2 * 2 = 9
x₁ = (-b-√D)/2a = (5 - 3)/4 = 0,5
x₂ = (-b+√D)/2a = (5 + 3)/4 = 2
ответ: при x = 0,5 и x = 2.
в) Принадлежит ли графику функции точка A(1;0).
0 = 2 * 1² - 5 * 1 + 3
0 = 2 - 5 + 3
0 = 0
Значит, точка A(1;0) ∈ графику функции.
Функция задана формулой f(x) = 2x - 8
a) Определите, при каких значениях x f(x) > 0.
f(x) > 0
2x - 8 > 0
2x > 8
x > 4
При x ∈ (4; +∞) функция больше 0.
ответ: при x ∈ (4; +∞)
б) Найдите нули функции.
Нуль функции - место, где график функции пересекается с осью Ох. Приравняем к 0:
2x - 8 = 0
2x = 8
x = 4
ответ: 4
Найдите область определения функции:
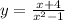
Найти область определения функции - значит найти значения, при которых функция имеет смысл.
Заметим, что если знаменатель будет равен нулю - функция бессмысленна. Тогда:
x² - 1 ≠ 0
x² ≠ 1
x ≠ ± 1
Область определения (ОДЗ): x ∈ ( - ∞; -1) ∪ (-1; 1) ∪ (1; + ∞).
удачи :D