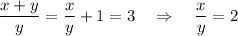и тогда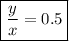 
Объяснение:
Вопрос 1.
Такую функцию называют обратимой.
Обратимой называется функция в которой произвольному значению функции соответствует единственное значение аргумента.
Вопрос 2.
Исходная обратимая функция и функция, полученная из нее путем замены x на y и y на x, называются обратными.
у=5х+2
х=5у+2
5у=х-2
у=0,2(х-2)
Вопрос 3.
Строго монотонная функция обратима.
Да, является.
Вопрос 4.
Обратимые функции:
у=5х+2
у=х⁵
у=х³+1
Если найти производную каждой фцнкции, то выяснится, что функции монотонны, а заначит обратимы.
Установите соответствие между функциями и характеристиками этих функций на отрезке [0; 2].
1) Функция принимает отриц значение в каждой точке отрезка[0; 2]
2) Функция возрастает на отрезке [0; 2]
3) Функция принимает полож. значение в каждой точке отрезка [0; 2]
4) Функция убывает на отрезке [0; 2]
Объяснение: ( Г "странная" функция).
А Б В Г
1)у<0 в каждой точке [0; 2] - + + -
2) Bозрастает на [0; 2] - + + -
3) y>0 в каждой точке [0; 2] + - - +
4) Убывает на отрезке [0; 2] + - - +
