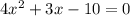, если их несколько, то указать сумму. 
): 
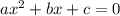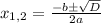, дискриминант же расписывается по-своему: 
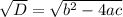. Дискриминант как бы заслужил своё отдельное внимание, ведь именно при его вычислении люди нередко допускают ошибки. Теперь – решаем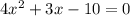, отсюда: 
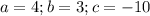, значит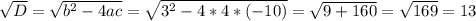
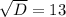; это как в алгебраических выражений седьмого класса – ты складываешь буквы, подставляешь вместо них какие-то числа и считываешь ответ, так вот здесь тоже самое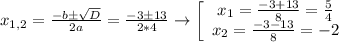
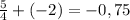
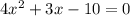равна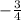 
Составим уравнение:
30/(5-х) +30/(5+х) = 12,5;
30(5+х) + 30(5 -х) = 12,5*(5-х)(5+х);
150 +30х ++150 -30x= 12,5(25 - x^2);;
300=12,5*25 - 12,5 x^2;
12,5 x^2=12,5;
x^2=1;
x=1.
проверка: По течению лодка плыла 30 км со скорость 5+1=6 км/ч и потратила на это 30/6=5 часов, против течения лодка плыла со скорость 5-1=4 км/ч и потратила всего 30/4=7,5 часов. В сумме получается 5 + 7,5 =12, 5 часов. ОТвет ; скорость течения равна 1 км/ч