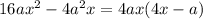
1) Найдем первые члены последовательности
b(1)=1^2-4=-3
b(2)=2^2-4=0
b(3)=3^2-4=5
b(4)=4^2-4=12
b(5)=5^2-4=21
последовательность возроастающая, значит следующие члены будут большими за 21
значит нам подходят только -3, 0, 21
можно было иначе -3=n^2-4 откуда натуральное n равно 1
6=n^2-4 такого натурального n нет
0=n^2-4 откуда натуральное n равно 2
21=n^2-4 откуда натуральное n равно 5
второй вариант поиска более верный, но у нас небольшие числа можно искать и по первому)
2) знаменатель равен b2\b1 или b3\b2 и так далее ,то есть отношению следующего члена прогрессии к предыдущему
b1=3 b2=1 b3=1\3 ...
значит он равен 1\3
ответ г)1/3
3) ищем знаменатель 1\3 : 1\6 =2 q=b2\b1
значит х =1\3 *2=2\3 b3=b2*q
ответ: 2\3
Построим график функцииy=|x+2|+|x-2|y=∣x+2∣+∣x−2∣
Для начала упростим функцию
Найдем знаки под модульного выражения
\begin{gathered} \left[\begin{array}{ccc}x+2=0\\ x-2=0\end{array}\right\Rightarrow \left[\begin{array}{ccc}x_1=-2\\ x_2=2\end{array}\right\end{gathered}
_-__-__(-2)__+__-__(2)__+__+__
\begin{gathered}y=|x+2|+|x-2|= \left[\begin{array}{ccc} \left \{ {{x \leq -2} \atop {-x-2-x+2}} \right. \\ \left \{ {{-2\ \textless \ x \leq 2} \atop {x+2-x+2}} \right. \\ \left \{ {{x\ \textgreater \ 2} \atop {x+2+x-2}} \right. \end{array}\right= \left[\begin{array}{ccc} \left \{ {{x \leq -2} \atop {-2x}} \right. \\ \left \{ {{-2\ \textless \ x \leq 2} \atop {4}} \right. \\ \left \{ {{x\ \textgreater \ 2} \atop {2x}} \right. \end{array}\right\end{gathered}
Наименьшее положительное значение параметра а найдем с параллельности прямых
График функции y=|x+2|+|x-2|y=∣x+2∣+∣x−2∣параллельный прямой y-ax+a-3=0y−ax+a−3=0 если угловые коэффициенты будут совпадать, т.е. k=\pm2k=±2
Но нам важен положительный параметр, значит a=2a=2 - минимальный.
Исследуем когда график будет касаться в точке (2;4) и (-2;4)
Подставив значения х=2 и у=4, получим
\begin{gathered}4-2a+a-3=0\\ 1-a=0\\ a=1\end{gathered}4−2a+a−3=01−a=0a=1
При а=1 система уравнений имеет одно решение
Если подставить x=-2x=−2 и y=4y=4 , получим
\begin{gathered}4+2a+a-3=0\\ 3a=-1\\ a=- \frac{1}{3} \end{gathered}4+2a+a−3=03a=−1a=−31
Наименьший параметр а=1.