.
Объяснение:
Обозначим центры окружностей, описанных около треугольников ADB и ADC через O1 и O2, а середины отрезков BD, DC, MN, DO2 и O1O2 — через A1, A2, K, E и O соответственно (см. рис.). Пусть ∠ BAD = ∠ CAD = α . Тогда ∠ A1O1D = ∠ A2O2D = α (так как половина центрального угла равна вписанному, опирающемуся на ту же дугу). Отрезок OK — средняя линия трапеции (или прямоугольника) O1MNO2, следовательно, OK ⊥ l, и (фото сверху). Заметим, что точки E, O и A2 лежат на одной прямой, так как ∠ OEO2 + ∠ O2EA2 = ∠ O1DO2 + ∠ O2EA2 = ∠ O1AO2 + (180° – ∠ DO2C) = 2 α + (180° – 2 α ) = 180°, т.е. OK = OE + EA2 = OA2. Аналогично доказывается, что OA1 = OK. Значит, точки A1, A2 и K лежат на окружности с центром O, а так как OK ⊥ l, то эта окружность касается прямой l.
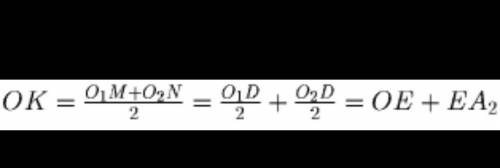
ответ: 20 км/час.
Объяснение:
Велосипедист выехал с некоторой скоростью из пункта А в пункт В, расстояние между которыми 60 км Прибыв в пункт в, он повернул назад и ехал с той же скоростью, а через час сделал на 20 мин. После этого велосипедист увеличил скоростью на 4 км/ч. Найдите начальную скорость велосипедиста, если расстояние от В до А он проехал за то же время, что и от А до В.
Решение.
Пусть х км/час - начальная скорость велосипедиста. Тогда
путь от А до В он проехал за t1=60/x часов.
На обратном пути он проехал за 1 час х км, 20 минут(1/3 часа) отдыхал и оставшийся путь проехал со скоростью x+4 км/час за время (60-x)/(x+4) часа. Таким образом на обратный путь он затратил t2=1+1/3+ (60-x)/(x+4) часа.
По условию t1=t2. Тогда
60/x= 4/3+ (60-x)/(x+4);
3*60(x+4)=4*x(x+4)+3*x(60-x);
180x+720=4x²+16x+180x-3x²;
x²+16x-720=0;
По т. Виета
x1+x2=-16; x1*x2=-720;
x1=20; x2=-36 - не соответствует условию.
x=20 км/час - первоначальная скорость велосипедиста.
Объяснение:
1) (ab)^10/(a^9b^8) *a²=(a^10b^10/(a^9b^8) *a²=ab²*a²=a³b²
3)
((k^6)^7*(t^3)^9 /( (k^7*t^4)³)²= k^42*t^27/(k^21*t^12)² =
=k^42*t^27 / k^42*t^24= t³