Объяснение:
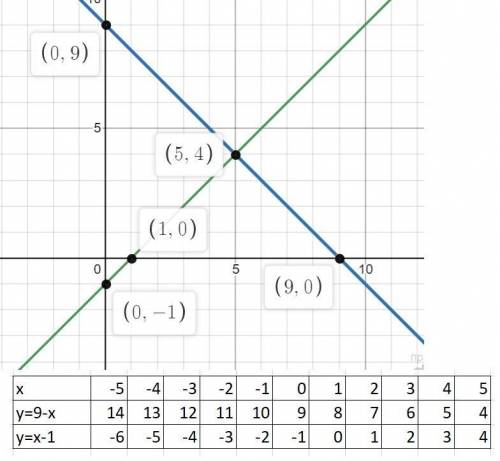
1) x+y=9; y=9-x;
x-y=1. y=x-1;
Составляем таблицу значений изменения функций при изменении аргумента и строем графики. Точка пересечения и является решением: (5;4)
(См. скриншот)
-------------
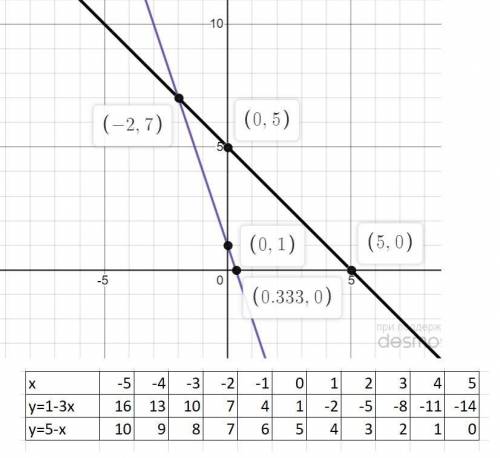
2) 3x+y=1; y=1-3x
x+y=5; y=5-x.
Составляем таблицу значений изменения функций при изменении аргумента и строем графики. Точка пересечения и является решением: (-2;7)
(См. скриншот)
---------------------
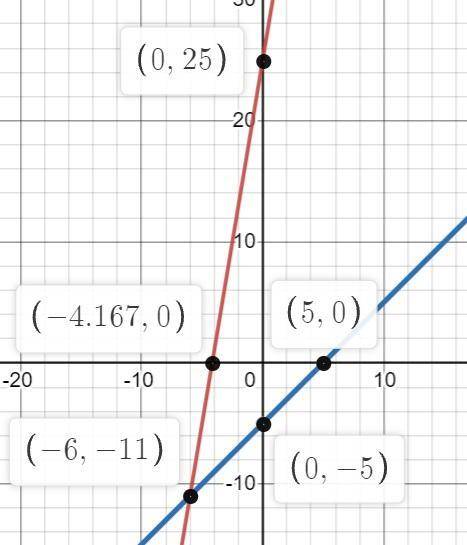
3) y-6x=-25; y=25+6x;
y-x=-5; y=x-5;
Составляем таблицу значений изменения функций при изменении аргумента и строем графики. Точка пересечения и является решением: (-6;-11)
(См. скриншот)
------------------------
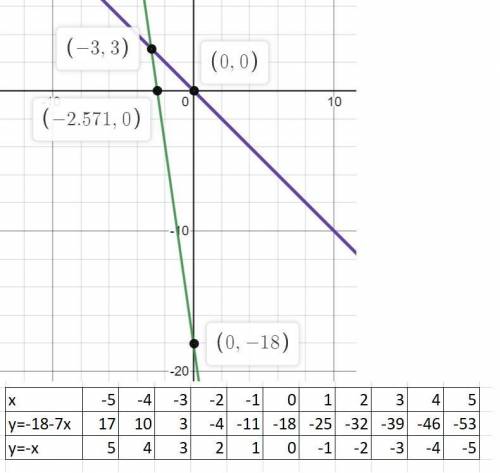
4) y+7x=-18; y=-18-7x;
y+x=0; y=-x;
Составляем таблицу значений изменения функций при изменении аргумента и строем графики. Точка пересечения и является решением: (-3;3)
(См. скриншот)
8*x²-14*x*y+14*y²=8
21*x²+14*x*y-14*y²=21
2) Складывая полученные уравнения, приходим к уравнению 29*x²=29. Отсюда x²=1,x1=1, x2=-1.
3) Подставляя x1=1 в первое уравнение исходной системы, получаем уравнение 4-7*y+7*y²=4, или y²-y=0. Отсюда y1=0, y2=1 и мы находим первые две пары решений системы: (1,0) и (1,1)
4) Подставляя теперь x2=-1 в первое уравнение системы, получаем уравнение 4+7*y+7*y²=4, или y²+y=0. Отсюда y3=0, y4=-1 и мы находим другие две пары решений системы: (-1,0) и (-1,-1).
5) Из всех 4-х пар решений наибольшую сумму имеет вторая. Обозначая x0=1 и y0=1, находим x0+y0=2.
ответ: 2