
![\int (2x-3)\, dx=[t=2x-3\;,\; dt=d(2x-3)=(2x-3)'\, dx=2\, dx,\\\\dx=\frac{dt}{2}\, ]=\frac{1}{2}\cdot \int t\cdot dt=\frac{1}{2}\cdot \frac{t^2}{2}+C=\frac{1}{4}\cdot (2x-3)^2+C;\; \; \to \\\\\int _{-3}^2(2x-3)\, dx=\frac{1}{4}\cdot (2x-3)^2\, |_{-3}^2=\frac{1}{4}\cdot (1^2-(-9)^2)=\\\\=\frac{1}{4}\cdot (1-9)=-2](/tpl/images/0624/4857/fe06b.png)
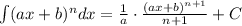
y = ax² + n
Найдем a, n для следующих случаев:
а) Найдем n:
n = y - ax²
При x = 0, y = 0, n = y, (см. рис):
n = y(0) = 0
Найдем a:
a = (y - n)/x²
При x = 1, a = y - n, (см. рис):
а = y(1) - n = 1 - 0 = 1
Следовательно, имеем a = 1, n = 0
функция имеет вид: y = x².
б) Найдем n:
n = y - ax²
При x = 0, n = y, (см. рис):
n = y(0) = -4
Найдем a:
a = (y - n)/x²
При у = 0, x = ±4, a = -n/x², (см. рис):
а = -(-4)/(±4)² = 4/16 = ¼
Следовательно, имеем a = ¼, n = -4
функция имеет вид: y = ¼x² - 4.
в) Найдем n:
n = y - ax²
При x = 0, n = y, (см. рис):
n = y(0) = 3
Найдем a:
a = (y - n)/x²
При x = ±2 , y = -5, (см. рис):
а = (-5 - 3)/(±2)² = -8/4 = -2
Следовательно, имеем a = -2, n = 3
функция имеет вид: y = -2x² + 3.