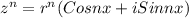
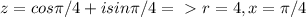
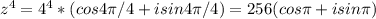
![z=r*[cos(\phi)+i*sin(\phi)]\\\\ z^n=(r*[cos(\phi)+i*sin(\phi)])^n=r^n*[cos(n\phi)+i*sin(n\phi)]\\\\\\ (4*[cos(\frac{\pi}{4})+i*sin(\frac{\pi}{4})])^4=4^4*[cos(4*\frac{\pi}{4})+i*sin(4*\frac{\pi}{4})]=\\\\ =256*[cos(\pi)+i*sin(\pi)].](/tpl/images/0916/0529/f55c8.png)
Пусть первое число равно х, тогда второе число равно (17 - х). Квадрат первого числа равен х^2, а квадрат второго числа равен (17 - х)^2. По условию задачи известно, что сумма квадратов этих двух чисел равна (х^2 + (17 - х)^2) или 185. Составим уравнение и решим его.
х^2 + (17 - х)^2 = 185;
х^2 + 289 - 34х + х^2 = 185;
2х^2 - 34х + 289 - 185 = 0;
2х^2 - 34х + 104 = 0;
х^2 - 17х + 52 = 0;
D = b^2 - 4ac;
D = (-17)^2 - 4 * 1 * 52 = 289 - 208 = 81; √D = 9;
x = (-b ± √D)/(2a);
x1 = (17 + 9)/2 = 26/2 = 13 - первое число;
х2 = (17 - 9)/2 = 8/2 = 4 - первое число;
17 - х1 = 17 - 13 = 4 - второе число;
17 - х2 = 17 - 4 = 13 - второе число.
ответ:a<-1/12
Объяснение:
Рассмотрим функцию f(x)=sqrt(3a+x), тогда уравнение примет вид
f(f(x))=x
Поскольку функция f(x) монотонно возрастает, то исходное уравнение равносильно уравнению f(x)=x
sqrt(3a+x)=x, x>=0
3a+x=x^2
x^2-x-3a=0
D=1+12a
Найдем при каких а, получившееся квадратное уравнение имеет хотя бы один неотрицательный корень. Для этого достаточно чтобы больший корень был неотрицателен.
x=(1+sqrt(1+12a))/2>=0 <=> sqrt(1+12a)>=-1
Выходит, что если получившееся квадратное уравнение имеет хотя бы одно решение, то оно будет неотрицательно.
Значит, единственный случай, который нам подходит, это когда квадратное уравнение корней не имеет.
D=1+12a<0 <=> a<-1/12