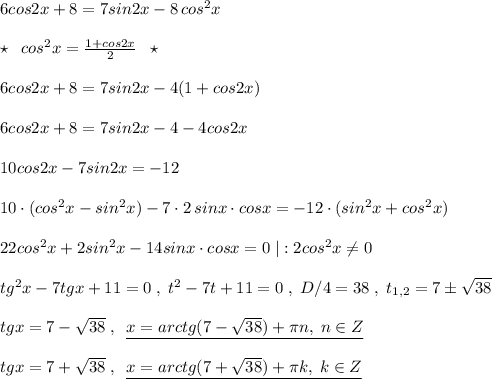
3 в 975 степени
Объяснение:
=1560354765479408771070917553392633760537768868829341902286239641295619538126878611383020598366063879052743737850141576125376939132860022759975937127922149991229384955750896054452170526119575506063977370113855316896737652742795594780624647445528643777767720449283627965512870320760841650498823733252782609272453434643167391789289665566190287412557742860345498697098992061814668957215730925421245856294165222381473651941745005808472220444538010040779712545464848147307
Последняя цифра 7