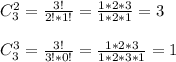Напишите уравнение касательной к графику функции f(x)=(4x+3)^5 в точке х0, если х0-абцисса точки пересечения графика функуии f(x)=(4x+3)^5 и прямой у= -1

👇

Увидеть ответ

Ответ:

utseetstse

30.12.2021

Напишите уравнение касательной к графику функции f(x)=(4x+3)^5 в точке х0, если х0-абцисса точки пер

4,5(91 оценок)

Открыть все ответы

Ответ:

mlgcuca

30.12.2021

Аппликация состоит из двух полосок.

1) Если Наташа хочет сделать аппликацию из полосок разного цвета и не имеет значения, как расположены полоски, то вариантов только 3.

Сочетание цветов : жёлтый-красный, жёлтый-синий, красный-синий.

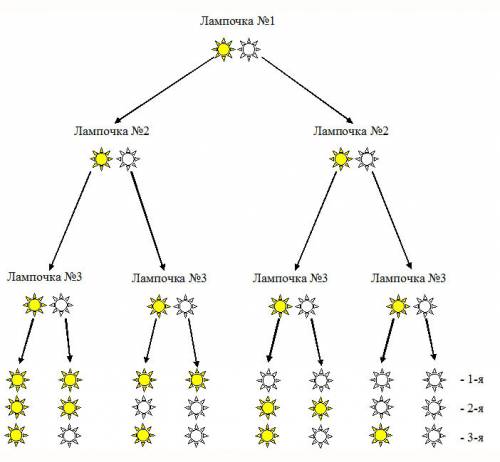
2) Если Наташа хочет сделать аппликацию из полосок разного цвета и имеет значение, как расположены полоски, то вариантов 6 ( см.рис).

Сочетание цветов : жёлтый-красный, красный-жёлтый, жёлтый-синий, синий-жёлтый, красный-синий, синий-красный.

3) Если Наташа хочет сделать аппликацию из полосок любого цвета и не имеет значения, как расположены полоски, то вариантов 6.

Сочетание цветов : жёлтый-жёлтый, красный-красный, синий-синий, жёлтый-красный, жёлтый-синий, красный-синий.

4) Если Наташа хочет сделать аппликацию из полосок любого цвета и имеет значение, как расположены полоски, то вариантов 9.

Сочетание цветов : жёлтый-жёлтый, красный-красный, синий-синий, жёлтый-красный, красный-жёлтый, жёлтый-синий, синий-жёлтый, красный-синий, синий-красный.

ответ: В зависимости от того, какой хочет видеть аппликацию Наташа, ей придётся выбирать из 3, 6 или 9 вариантов.

Наташа хочет сделать аппликацию на платье из двух цветных вертикальных полос. из скольких вариантов

4,4(57 оценок)

Ответ:

dfghjkghjkl

30.12.2021

Дерево возможных вариантов см. на рисунке. Отсюда наглядно виды все решения.

а) Сколько имеется различных освещения коридора, включая случай когда все лампочки не горят. Как видим, каждая лампочка имеет два состояния (горит/не горит). Т.к. лампочек три, то всего вариантов будет 2³ = 8. Все 8 вариантов представлены на рисунке.

б) Сколько имеется различных освещения, если известно что лампочки №1 и №2 горят или не горят одновременно? Когда лампочки №1 и №2 горят, то лампочка №3 либо горит, либо не горит (2 варианта). Точно также, когда лампочки №1 и №2 не горят, то лампочка №3 тоже либо горит, либо не горит (2 варианта). Итого, 4 варианта. Проверяем по рисунку.

в) Сколько имеется различных освещения, если известно что при горящей лампочке №3 лампочка №2 не горит?
По рисунку считаем варианты - их 6. Когда лампочка №3 горит, то лампочка №2 не горит (по условию), а у лампочки №1 есть 2 варианта - горит/не горит. Когда лампочка №3 не горит, то вариантов у оставшихся лампочек будет 2² = 4. Вот и получается 6 вариантов.

г) сколько имеется различных освещения коридора когда горит большинство лампочек? Т.е. нам надо сосчитать случаи, когда одновременно горят 2 и более лампочек. По рисунку высчитываем, что есть 4 варианта. Или считаем число сочетаний двух лампочек из трёх, плюс число сочетаний три лампочки из трёх.
$C_3^2 = \frac{3!}{2!*1!} = \frac{1*2*3}{1*2*1} = 3 \\ \\ C_3^3 = \frac{3!}{3!*0!} = \frac{1*2*3}{1*2*3*1} = 1$
Итак, 4 варианта.
Вкоридоре 3 лампочки а) сколько имеется различных освещения коридора,включа случай когда все лампочк