1) 6x^2 - 12 = 0
6(x^2 - 2) = 0
x^2 = 2
x = ±√2
2) 3a^2 + 5a + 2 = 0
D = b^2 - 4ac = 25 - 4 * 3 * 2 = 25 - 24 = 1, √D = 1.
a1 = (-5 + 1) / 6 = -4/6 = -2/3
a2 = (-5 - 1) / 6 = -1
3) 4x + 4x^2 + 1 = 0
4x^2 + 4x + 1 = 0
D = k^2 - ac (вторая формула для нахождения дискр.) = 2^2 - 4*1 = 0
x1 = -2 + 0 / 4 = -0,5
4) 3x^2 + 7x - 6 = 0
D = b^2 - 4ac = 49 - 4 * 3 * (-6) = 49 +72 = 121, √D = 11
x1 = -7 + 11 / 6 = 4/6 = 2/3
x2 = -7 - 11 / 6 = -3
5) 5x^2 - 22x - 15 = 0
D = k^2 - ac = 11^2 - 5 * (-15) = 121 + 75 = 196, √D = 14
x1 = 11 + 14 / 5 = 25 / 5 = 5
x2 = 11 - 14 / 5 = -3/5 = - 0,6
6) 3x^2 - 10x + 9 = 0
D = k^2 - ac = 25 - 3 * 9 = 25 - 27 = -2, √D < 0, корней нет.
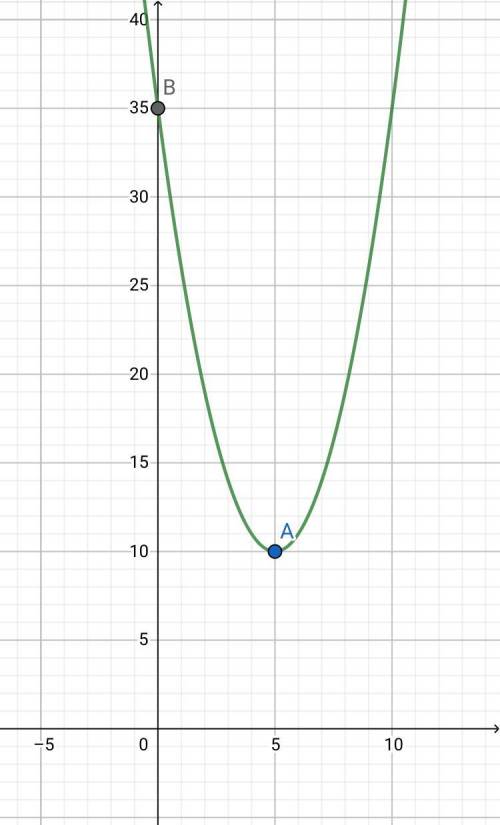
f(x) = (x-5)² + 10 = x² - 10x + 35
а) Высоту? Это как понять. Парабола не имеет высоты. Парабола бесконечна, начиная от вершины.
Возможно, Вы имели в виду найти вершину параболы?
Вершина параболы - точка А(х₀; у₀)
х₀ = -b/2a = 10/2 = 5
у₀ = f(х₀) = 10
A(5; 10)
b) f(x) = (x-5)² + 10
(x-5)² <— это значит что функция х² смещена на пять единиц вправо
Соответсвенно, ось симметрии будет иметь вид:
х = 5
с) f(x) = 0
(x-5)²>= 0
(x-5)² + 10 >= 10
А значит, значение функции попросту не может быть равно 0.
То есть, точек пересечения с осью Ох нет.
d) х = 0
f(x) = x² - 10x + 35 = 35
Точка пересечения с осью Оу - точка В
В(0; 35)
e) —> в прикрепленном файле