Объяснение:
Периметр прямоугольника есть удвоенная сумма двух его смежных сторон, т.е. P = 2(a+b)
Площадь есть произведение двух его смежных сторон, то есть S = ab
Тогда имеем систему уравнений:
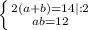
Разделим первое уравнение на 2, и будем иметь то, что Вам и нужно - теорему Виета!
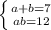
Точнее, такую же систему, какую имеем в теореме Виета для приведенного кв. уравнения, у которого есть два корня.
Здесь решения системы легко подбираются: a = 3, b = 4 (или наоборот, т.к. система относительно переменных симметрична).
Но мы все же решим методом подстановки, ибо не у всех могут учителя принять метод подбора (метод "пристального взгляда", так сказать).
Выразим из первого уравнения a:
a = 7 - b.
Подставим его во второе уравнение:
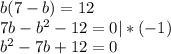
Назовем b = x, чтобы не путаться, где у нас неизвестное, а где - коэф. кв. трехчлена.
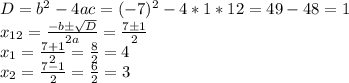
При x1 = b1 = 4 имеем a1 = 7 - b1 = 7 - 4 = 3
При x2 = b2 = 3 имеем a2 = 7 - b2 = 7 - 3 = 4
А значит имеем 2 корня:
a = 3
b = 4
Вернемся к прямоугольнику. a и b - это его стороны, а значит a = 3см и b = 4 см.
ответ: стороны прямоугольника равны 3 см и 4 см.
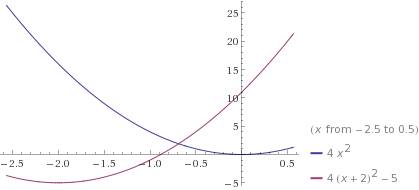
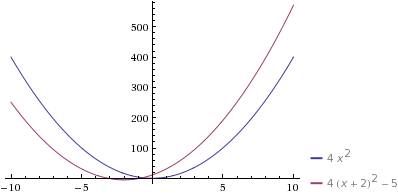
если для первого графика y = 4x^2 вершина находится в точке (0;0), то
ось симметрии параболы - ось OY (уравнение x=0)
то для второго графика ось симметрии сместится влево на 2 (уравнение x = -2, все первое слагаемое обратится в 0 и получится y = -5), т.е. для второго графика вершина опустится вниз по оси OY на 5 единиц и сместится влево на 2 единицы по оси OX
координаты вершины новой параболы (-2;-5), ветви вверх и она в точности повторяет первый график (из новой точки---новой вершины), иными словами
новый график получится параллельным переносом исходного графика вниз по оси OY на 5 единиц и влево по оси OX на 2 единицы