При упрощении используем sin2a=2sinacosa
Если в числителе вынести 2sina, а в знаменателе 2cosa, то останутся скобки (sina+cosa), которые сократятся
Останется sina/cosa=tga
ctga=1/4, значит tga=4
Объяснение:
Функция задана формулой y = −3x + 1. Определите:
1) значение функции, если значение аргумента равно 4;
2) значение аргумента, при котором значение функции равно −5;
3) проходит ли график функции через точку A (−2; 7).
1)y = −3x + 1
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Таблица:
х -1 0 1
у 4 1 -2
а)Чтобы найти значение у, нужно известное значение х подставить в уравнение и вычислить у:
х=4
у= -3*4+1= -11 при х=4 у= -11
б)Чтобы найти значение х, нужно известное значение у подставить в уравнение и вычислить х:
у= -5
-5= -3х+1
3х=1+5
3х=6
х=2 у= -5 при х=2
в)Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение, если левая часть будет равна правой, значит, точка принадлежит графику и наоборот.
A (−2; 7)
y = −3x + 1
7= -3*(-2)+1
7=6+1
7=7, проходит.
2)Постройте график функции y = 2x − 5. Пользуясь графиком, найдите:
1) значение функции, если значение аргумента равно 3;
2) значение аргумента, при котором значение функции равно −1.
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
y = 2x − 5
Таблица:
х -1 0 1
у -7 -5 -3
б)согласно графика, при х=3 у=1
согласно графика у= -1 при х=2
3)Не выполняя построения, найдите координаты точек пересечения
графика функции y = −0,6x + 3 с осями координат.
а)График пересекает ось Оу при х=0:
х=0
у= -6*0+3=3
Координаты точки пересечения графиком оси Оу (0; 3)
б)График пересекает ось Ох при у=0.
у=0
0= -0,6х+3
0,6х=3
х=5
Координаты точки пересечения графиком оси Ох (5; 0)
4)При каком значении k график функции y = kx+ 5 проходит через точку D (6; −19)?
Подставляем известные значения х и у (координаты точки D) в уравнение и вычисляем k:
y = kx+ 5
-19=k*6+5
-6k=5+19
-6k=24
k= -4
Найти допустимые значения переменной в дроби, значит найти значения переменой, при которой знаменатель не равен 0
1)
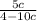 , значит знаменатель 4-10с не может быть равен 0, отсюда
, значит знаменатель 4-10с не может быть равен 0, отсюда
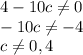
Значит с - любое число, кроме 0,4
2)
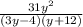 , значит знаменатель (3у-4)(у+12) не может быть равен 0, отсюда
, значит знаменатель (3у-4)(у+12) не может быть равен 0, отсюда
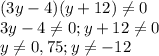
Значит у - любое число, кроме 0,75 и -12
3)
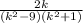 , значит знаменатель (k²-9)(k²+1) не может быть равен 0, отсюда
, значит знаменатель (k²-9)(k²+1) не может быть равен 0, отсюда
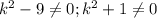
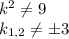
k²+1 никогда не будет равен 0, т.к. никакое число в квадрате не будет отрицательным
Значит k - любое число, кроме 3 и -3
распишем двойные углы: (sin(2a) = 2sinacosa, sin(2a) = 2tga/(1+tg²a))
2sin² a + sin(2a)/2cos²a + sin(2a) = 2sin² a + 2sinacosa/2cos²a + 2tga/(1+tg²a) = 2sin²a + tga + 2tga/(1+tg²a)
ctg a = 1/4 значит tg a = 4
ctg²x+1=1/sin²x выразим из формулы sin²x = 1/(ctg²x+1) = 1/(1/16+1) = 16/17
подставляем:
2sin²a + tga + 2tga/(1+tg²a) = 32/17 + 4 + 8/17 = 108/17