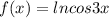
f'(x)=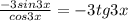
f'(П/9)=-3*tgП/3=-3√3
чтобы наибольшее значение данной функции было не меньше 1, необходимо и достаточно, чтобы она в какой-то точке приняла значение 1.
если наибольшее значение функции не меньше единицы, то по непрерывности в какой-то точке будет значение единица. если же наибольшее значение меньше единицы, то значение единица приниматься не может. значит нужно найти при каких значениях a есть корни у уравнения |x - a| = x² + 1
так как x² + 1 > 0 , то уравнение равносильно совокупности :
эта совокупность имеет решение, если:
ответ:
х(приблизно дорівнює)
все готово удачі там тобі надіюся що воно тобі то постав як найкращу відповідь будь-
f'(x)=ln(cos3x)=(3x)'*(cos3x)'*(lncos3x)'=3*(-sin3x)*(1/cos3x)=-3sin3x/cos3x=-3tg3x
при х=п/9, f'(x)=f'(п/9)=-3(tg(п/3))=-3*корень квадратный из 3