1
x>0,y>0
{x²+y²=5
{log(2)x+log(2)y=1⇒log(2)xy=1⇒xy=2⇒2xy=4
прибавим
x²+y²+2xy=9
(x+y)²=9
a)x+y=-3
x=-3-y
-3y-y²=2
y²+3y+2=0
y1+y2=-3 U y1*y2=2
y1=-2 не удов усл
у2=-1 не удов усл
б)x+y=3
x=3-y
3y-y²=2
y²-3y+2=0
y1+y2=3 U y1*y2=1
y1=1⇒x1=2
y2=2⇒x2=1
(2;1);(1;2)
2
x>0,y>0
{x²-y²=12
log(2)x-log(2)y1⇒log(2)(x/y)=1⇒x/y=2⇒x=2y
4y²-y²=12
3y²=12
y²=4
y1=-2 не удов усл
y2=2⇒x=4
(4;2)
3
x>0,y>0
{x²+y²=25
lgx+lgy=lg12⇒xy=12⇒2xy=24
x²+y²+2xy=49
(x+y)²=49
a)x+y=-7
x=-y-7
-y²-7y=12
y²+7y+12=0
y1+y2=-7 U y1*y2=12
y1=-3 не удов усл
y2=-4 не удов усл
б)x+y=7
x=7-y
7y-y²=12
y²-7y+12=0
y1+y2=7 U y1*y2=12
y1=3⇒x1=4
y2=4⇒x2=3
(4;3);(3;4)
4
x>0 y>0
{log(0,5)xy=-1⇒xy=2
{x=3+2y
3y+2y²-2=0
D=9+16=25
y1=(-3-5)/4=-2 не удов усл
у2=(-3+5)/4=0,5⇒х=4
(4;0,5)
При каких значениях параметра p система уравнений
имеет три решения?
Графический решения:
Уравнение окружности имеет вид:
1-е уравнение задаёт окружность с цетром в точке A(0;0) и радиусом 6
2-е уравнение задаёт параболу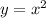
, смещённую на p по ординате.
p<-36 - нет решений
p=-36 - 2 решения
-36<p<-6 - 4 решения
p=-6 - 3 решения
-6<p<6 - 2 решения
p=6 - 1 решение
p>6 - нет решений
ответ: p=-6