В решении.
Объяснение:
Постройте график функции у. Найдите вершину и ось симметрии параболы и опишите свойства функции.
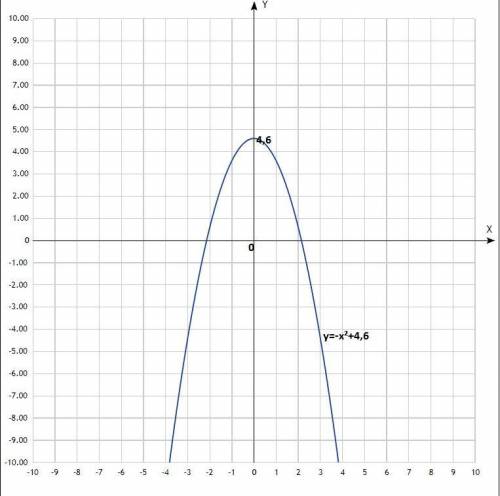
2) у = -х² + 4,6;
Уравнение квадратичной функции, график - классическая парабола у = х² со сдвигом по оси Оу вверх на 4,6 единицы, ветви направлены вниз.
а) Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -3 -2 -1 0 1 2 3
у -4,4 0,6 3,6 4,6 3,6 0,6 -4,4
По вычисленным точкам построить параболу.
б) Вычислить вершину параболы:
Формула: х₀ = -b/2a;
у = -х² + 4,6;
х₀ = 0/-2
х₀ = 0;
у₀ = 0² + 4,6
у₀ = 4,6;
Координаты вершины параболы: (0; 4,6).
в) Вычислить ось симметрии:
Х = х₀;
Х = 0.
г) Свойства квадратичной функции у = -х² + 4,6:
1) Областью определения функции является множество всех действительных чисел, т.е. D(у): (-∞; +∞);
2) Множеством значений функции является промежуток
Е(у): [4,6; -∞);
3) Значение функции y = 4,6 является наибольшим, а наименьшего значения функция не имеет.
4) Функция является четной, график симметричен относительно оси Оу.
5) Нули функции: х = -2,15; х = 2,15.
6) На промежутке х∈(0; +∞) функция убывающая, на промежутке х∈(-∞; 0) - возрастающая.
7) Функция принимает положительные значения на промежутке х∈(-2,15; 2,15);
8) Функция принимает отрицательные значения на промежутке х∈(-∞; -2,15)∪(2,15; +∞).
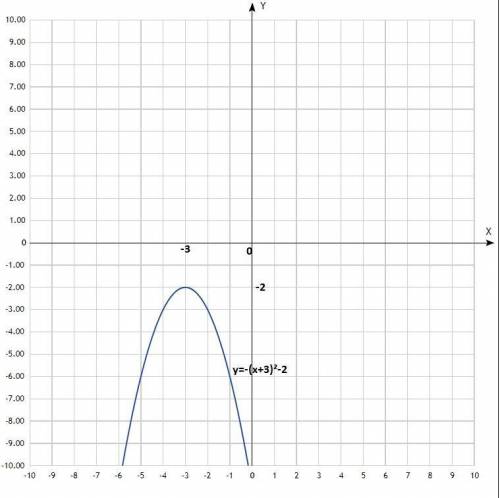
6) у = -(х+3)² - 2;
Уравнение квадратичной функции, график - классическая парабола у = х² со смещённым центром, со сдвигом по оси Ох влево на 3 единицы и сдвигом по оси Оу вниз на 2 единицы, ветви направлены вниз.
а) Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -5 -4 -3 -2 -1
у -6 -3 -2 -3 -6
По вычисленным точкам построить параболу.
б) Вычислить вершину параболы:
у = -(х + 3)² - 2;
у = -(х² + 6х + 9) -2
у = -х² - 6х - 9 - 2
у = -х² - 6х - 11;
Формула: х₀ = -b/2a;
х₀ = 6/-2
х₀ = -3;
у₀ = -(-3 + 3)² - 2
у₀ = -0² - 2
у₀ = -2;
Координаты вершины параболы: (-3; -2).
в) Вычислить ось симметрии:
Х = х₀;
Х = -3.
г) Свойства квадратичной функции у = -(х + 3)² - 2:
1) Областью определения функции является множество всех действительных чисел, т.е. D(у): (-∞; +∞);
2) Множеством значений функции является промежуток
Е(у): [-2; -∞);
3) Значение функции y = -2 является наибольшим, а наименьшего значения функция не имеет.
4) Функция общего вида. Не является ни чётной, ни нечётной.
5) Нулей функции нет: график ниже оси Ох, нет с ней пересечения.
6) На промежутке х∈(-3; +∞) функция убывающая, на промежутке х∈(-∞; -3) - возрастающая.
7) Функция не имеет положительных значений (график ниже оси Ох).
8) Функция принимает отрицательные значения на промежутке х∈(-∞; +∞).
1) D(y) =R;
2) E (y) =[–1;1];
3) Период функции равен ;
4) Функция чётная/нечётная;
5) Функция принимает:
значение, равное 0, при ;
наименьшее значение, равное –1, при ;
наибольшее значение, равное 1, при ;
положительные значения на интервале (0;) и на интервалах, получаемых сдвигами этого интервала на ;
отрицательные значения на интервале и на интервалах, получаемых сдвигами этого интервала на .
6) Функция
возрастает на отрезке и на отрезках, получаемых сдвигами этого отрезка на ;
убывает на отрезке и на отрезках, получаемых сдвигами этого отрезка на .
y=|x-1|+|x-3| , x≥ -1
Отметим нули выражений, находящихся под знаками модулей. Это х=1 и х=3. Вычислим знаки выражений, находящихся по знаками модулей, в трёх получившихся промежутках:
(х-1) : - - - (1) + + + (3) + + +
(х-3) : - - - (1) - - - - (3) + + +
Теперь рассмотрим, какой вид примет функция , в этих трёх промежутках.
1) -1≤ х≤1 : |x-1|=-(x-1)=1-x , |x-3|=-(x-3)=3-x ⇒ y=1-x+3-x , y=4-2x .
Cтроим прямую у=4-2х на промежутке х∈[-1, 1 ] .
2) 1<x≤3 : |x-1|=x-1 , |x-3|=-(x-3)=3-x ⇒ y=x-1+3-x , y=2.
Строим прямую у=2 на промежутке х∈(1,3 ] .
3) x>3 : |x-1|=x-1 , |x-3|=x-3 ⇒ y=x-1+x-3 , y=2x-4 .
Строим прямую у=2х-4 на промежутке х∈(3,+∞) .
График нарисован синим цветом на рисунке.