Разложите многочлен на множители (x+1)(x+3)(x+5)(x+7)+15

Question

Алгебра: Разложите многочлен на множители (x+1)(x+3)(x+5)(x+7)+15

Rou234 · Accepted Answer

Переформулируем условие в терминах арифметической прогрессии:

1) В первый день потратили 100 рублей = первый член прогрессии 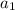a_1 равен 100.

2) Каждый последующий день тратили на 50 рублей больше = разность прогрессии 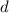равна 50.

3) Всего было 1000 рублей = сумма 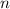членов (то есть 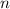дней) равна 1000.

Сумма вычисляется по формуле 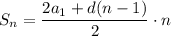$S_n=\dfrac{2a_1+d(n-1)}{2}\cdot n$

Чтобы найти 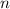, подставим в эту формулу известные числа:

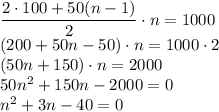
$\dfrac{2 \cdot 100+50(n-1)}{2} \cdot n=1000\\(200+50n-50) \cdot n = 1000 \cdot 2\\(50n+150) \cdot n=2000\\50n^2+150n-2000=0\\n^2+3n-40=0$

Решим это уравнение с дискриминанта:

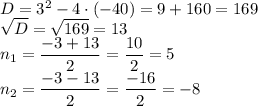
$D=3^2-4 \cdot (-40)=9+160=169\\\sqrt{D}=\sqrt{169}=13\\n_1=\dfrac{-3+13}{2}=\dfrac{10}{2}=5\\n_2=\dfrac{-3-13}{2}=\dfrac{-16}{2}=-8$

Количество дней не может быть отрицательным, поэтому имеем единственный ответ: 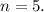n=5.

ответ: на пять дней.