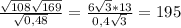Решение внизу на фото
Пусть х²+у²=к, ху=р, тогда к/р=34/15
к=34, подставим 34 вместо к в подстановку к/р=34/15, получим р=15
значит, ху=15, х²+у²=34, из первого уравнения у=15/х подставим во второе х²+у²=34, получим х²+(15/х)²=34, решим биквадратное уравнение.
х≠0, х⁴-34х²+225=0. Замена в=х², тогда в²-34в+225=0, по теореме, обратной теореме Виета, в₁=25, в₂=9, оба корня неотрицательные, поэтому, возвращаемся к замене в₁=х², х²=25, получим х₁=5; х₂=-5; если же в₂=9, то х²=9 и х₃=-3; х₄=3, соответственно ху=15, у₁=15/5=3, у₂=15/(-5)=-3; у₃=15/(-3)=-5; у₄=15/3=5
Искомые решения системы соберем в точки. (5;3);(-5;-3);(-3;-5);(3;5)
ответ (5;3);(-5;-3);(-3;-5);(3;5)
1)
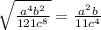при b ≥ 0.
2)
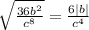
3)