ответ:
1) (3х + 1)/(х - 2) = (2х - 10)/(х + 1) - применим основное свойство пропорции: в верной пропорции произведение крайних членов пропорции равно произведению средних членов пропорции;
о. д. з. x ≠ 2; x ≠ -1;
(3х + 1)(х + 1) = (х - 2)(2х - 10);
3х^2 + 3х + х + 1 = 2х^2 - 10х - 4х + 20;
3х^2 + 4х + 1 = 2х^2 - 14х + 20;
3х^2 - 2х^2 + 4х + 14х + 1 - 20 = 0;
х^2 + 18х - 19 = 0;
d = b^2 - 4ac;
d = 18^2 - 4 * 1 * (-19) = 324 + 76 = 400; √d = 20;
x = (-b ± √d)/(2a);
x1 = (-18 + 20)/2 = 2/2 = 1;
x2 = (-18 - 20)/2 = -38/2 = -19.
ответ. 1; -19.
2) (х + 2)/(х - 1) + х/(х + 1) = 6/(х^2 - 1) - дроби в левой части уравнения к общему знаменателю (х - 1)(х + 1) = х^2 - 1; дополнительный множитель для первой дроби равен (х + 1), для второй - (х - 1);
((х + 2)(х + 1) + х(х - 1))/(х^2 - 1) = 6/(х^2 - 1) - чтобы дроби с одинаковыми знаменателями были равны, надо чтобы их числители тоже были равны;
о. д. з. х ≠ ±1;
(х + 2)(х + 1) + х(х - 1) = 6;
х^2 + х + 2х + 2 + х^2 - х - 6 = 0;
2х^2 + 2х - 4 = 0;
х^2 + х - 2 = 0;
d = 1^2 - 4 * 1 * (-2) = 1 + 8 = 9; √d = 3;
x1 = (-1 + 3)/2 = 2/2 = 1 - посторонний корень, т.к. не принадлежит о. д. з.;
x2 = (-1 - 3)/2 = -4/2 = -2.
ответ. -2.
объяснение:
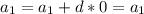проверено.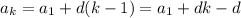
![a_{k+1}=a_1+d[(k+1)-1]=a_1+dk](/tpl/images/0582/6750/35dc7.png)
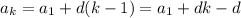то прибавив к данному выражению d. Мы получим следующий член .![S_n= \frac{n[2a_1+d(n-1)]}{2}](/tpl/images/0582/6750/67d86.png)
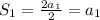. ![n=k \Rightarrow S_k= \frac{k[2a_1+d(k-1)]}{2}= \frac{2a_1k+dk^2-dk}{2}](/tpl/images/0582/6750/b9ca4.png)
:
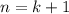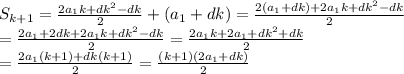
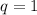получается деление на ноль, поэтому сразу пишем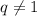 
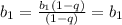
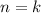
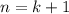:![b_{k+1}= \frac{b_1(1-q^k)}{1-q}+b_1q^k= \frac{(1-q)b_1q^k+b_1(1-q^k)}{1-q}\\= \frac{b_1[(1-q)q^k+(1-q^k)]}{1-q}= \frac{b_1[q^k-q^{k+1}+1-q^k]}{1-q}= \frac{b_1(1-q^{k+1})}{1-q}](/tpl/images/0582/6750/552be.png)
