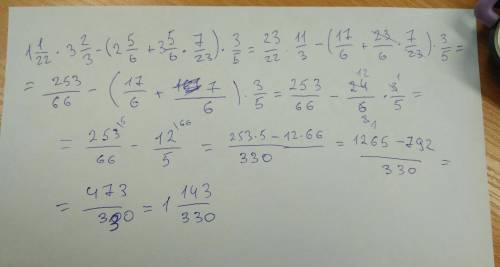
Алгебра: 11/22*3 2/3-(2 5/6+3 5/6*7/23)*3/5= решить в один длинный пример 20б

11/223 2/3-(2 5/6+3 5/67/23)*3/5= решить в один длинный пример 20б

👇

Ответ:

paradoksina

06.08.2020

Если мне не изменяет память по школьной программе и я правильно поняла какие условия, то ответ такой
11/22*3 2/3-(2 5/6+3 5/6*7/23)*3/5= решить в один длинный пример 20б

11/22*3 2/3-(2 5/6+3 5/6*7/23)*3/5= решить в один длинный пример 20б

4,8(36 оценок)

Открыть все ответы

Ответ:

fdglksjf

06.08.2020

Синус на промежутке $[ -\frac{\pi}{2} ; \frac{\pi}{2} ]$ возрастает, а на промежутке $[ \frac{\pi}{2} ; \frac{3\pi}{2} ]$ - убывает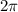

так как функция синуса периодична с периодом $2\pi$ , то:
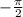$[ -\frac{\pi}{2}+2\pi n ; \frac{\pi}{2}+2\pi n ],n\in Z$ - промежутки возрастания синусоиды
и
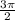$[ \frac{\pi}{2}+2\pi n ; \frac{3\pi}{2}+2\pi n ],n\in Z$ - промежутки убывания синусоиды

Что бы в этом убедится, предлагаю внимательно рассмотреть график синусоиды и/или тригонометрический круг

точка $- \frac{\pi}{2}$ и точка $\frac{3\pi}{2}$ - одна и та же точка на тригонометрическом круге

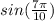Что бы ответить на вопросы задания, осталось посмотреть, в какие промежутки попадают углы:
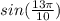
$sin( \frac{7\pi}{10} )$ и $sin( \frac{13\pi}{10} )$
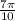
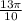
у нас углы $\frac{7\pi}{10}$ $\frac{13\pi}{10}$
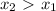оба угла попадают в промежуток $[ \frac{\pi}{2} ; \frac{3\pi}{2} ]$ убывания. Так как это промежуток убывания, то если выполняется $x_2\ \textgreater \ x_1$ , то будет выполнятся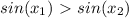 $sin(x_1)\ \textgreater \ sin(x_2)$
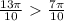
у нас: $\frac{13\pi}{10} \ \textgreater \ \frac{7\pi}{10}$
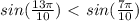
и тогда $sin(\frac{13\pi}{10})\ \textless \ sin(\frac{7\pi}{10})$

Суть разобрали, и дальше легче.
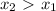Да и если углы из промежутка возрастания, то если $x_2\ \textgreater \ x_1$ , то выполняется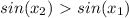 $sin(x_2)\ \textgreater \ sin(x_1)$
---------------------------------------
углы 13п/7 и 11п/7 оба попадают в промежуток возрастания $[ \frac{3\pi}{2} ; \frac{5\pi}{2}]$
значит sin( 13п/7 ) > sin ( 11п/7 )
--------------------------------------------
оба угла -8п/7 и -9п/8 попадают в интервал убывания $[- \frac{3\pi}{2} ; -\frac{\pi}{2} ]$
-8п/7 < -9п/8, по этому
sin(-8п/7) > sin(-9п/8)
----------------------------------------------
оба угла 7 и 6 попадают в промежуток возрастания $[ \frac{3\pi}{2} ; \frac{5\pi}{2} ]$
7 > 6
sin(7) > sin(6)

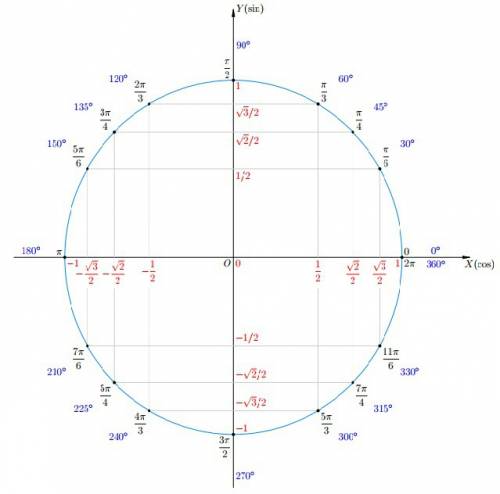
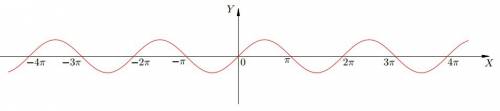
Используя свойство возрастания или убывания функции y=sinx сравнить числа: sin 7п/10 и sin 13п/10 si

Используя свойство возрастания или убывания функции y=sinx сравнить числа: sin 7п/10 и sin 13п/10 si

4,4(56 оценок)

Ответ:

TTe4enkaTyan

06.08.2020

Объяснение:

В этой задаче важно правильно расставить точки А, Б, В, Г на круге. Обратите внимание, они не обязательно должны идти по порядку! Общая логика такая. Самая большая дуга (в данном случае АБ=60) должна охватывать или точку Г или точку В (см. рисунок), иначе выстроить дуги не получится. В результате, точка А будет лежать напротив точки Б, а точки В и Г автоматически расположатся напротив друг друга (как показано на рисунке).

Далее, по условию задания точно можно обозначить длины дуг АГ=35 и АВ=45. Дуга АБ=60 может пройти как через точку Г, так и через точку В (это нужно выяснить). Аналогично, дуга ВГ может проходить или через точку Б, или через точку А.

Дуга АБ может проходить как через Г, так и через В (результаты должны получаться равными). Если АБ проходит через Г, то сегмент ГБ=60-35=25 и дуга ВБ=40-25=15. Если же дуга АБ проходит через В, то длина ВБ=60-45=15. Все верно.

4,6(56 оценок)

Это интересно:

Образование-и-коммуникации

27.10.2021

Как вести дневник: польза для здоровья и советы по созданию своего...

Стиль-и-уход-за-собой

01.12.2020

Как сделать неформальную стрижку: шаг за шагом инструкция для начинающих...

Дом-и-сад

22.01.2023

Как отремонтировать дом и создать уютное жилье?...

Финансы-и-бизнес