![1)\; \; \sqrt[3]{1-x}=2\; \; \to \; \; 1-x=2^3\; ,\; \; 1-x=8\; ,\; \; \underline {x=-7}\\\\2)\; \; \sqrt{x+3}=\sqrt{5-x}\; ,\; \; ODZ:\; \; \left \{ {{x+3\geq 0} \atop {5-x\geq 0}} \right. \; \left \{ {{x\geq -3} \atop {x\leq 5}} \right. \; \Rightarrow \; -3\leq x\leq 5\\\\x+3=5-x\; ,\; \; 2x=2\; ,\; \; \underline {x=1}](/tpl/images/0925/6260/c5d28.png)
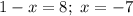
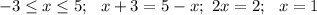
по примеру реши.
x^3 - 6x^2 + 11x - 6 = 0 можно, конечно, решить формулой кардано для решения кубических уравнений, но это долго и трудно. проще подобрать корни схемой горнера. возможные рациональные корни x = a/b, где а - делитель свободного члена, b - делитель старшего коэффициента. x = 1, -1, 2, -2, 3, -3, 6, -6 находишь значения в этих точках. y(1) = 1 - 6 + 11 - 6 = 0 - повезло сразу! теперь раскладываем: x^3 - x^2 - 5x^2 + 5x + 6x - 6 = 0 (x - 1)(x^2 - 5x + 6) = 0 (x - 1)(x - 2)(x - 3) = 0 ответ: x1 = 1, x2 = 2, x3 = 3