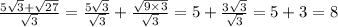
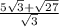
Разбиваем дробь
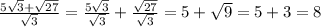
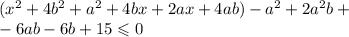
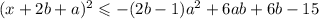
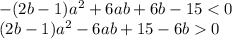
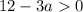
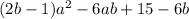должен принимать только положительные значения. Как известно, так будет, если: 1. Коэффициент при a^2 положительный и 2. Дискриминант отрицательный.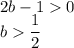
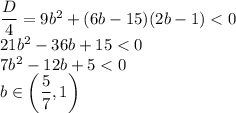
1)Решить систему уравнений методом подстановки.
а)Решение системы уравнений (-1; 4);
б)Решение системы уравнений (5; -1);
в)Решение системы уравнений (-1; -1).
2)Решить систему уравнений графически:
Координаты точки пересечения графиков функций (3; 1).
Решение системы уравнений (3; 1).
Объяснение:
1)Решить систему уравнений методом подстановки:
а)3х+у=1
2х-3у= -14
Выразим у через х в первом уравнении, подставим выражение во второе уравнение и вычислим х:
у=1-3х
2х-3(1-3х)= -14
2х-3+9х= -14
11х= -14+3
11х= -11
х= -1
у=1-3х
у=1-3*(-1)
у=1+3
у=4
Решение системы уравнений (-1; 4);
б)х+у=4
2х+7у=3
Выразим х через у в первом уравнении, подставим выражение во второе уравнение и вычислим у:
х=4-у
2(4-у)+7у=3
8-2у+7у=3
5у=3-8
5у= -5
у= -1;
х=4-у
х=4-(-1)
х=4+1
х=5;
Решение системы уравнений (5; -1);
в)2х-3(у+1)= -2
3(х+1)+3у=2у-1
Раскрыть скобки:
2х-3у-3= -2
3х+3+3у=2у-1
Привести подобные члены:
2х-3у=1
3х+у= -4
Выразим у через х во втором уравнении, подставим выражение в первое уравнение и вычислим х:
у= -4-3х
2х-3(-4-3х)=1
2х+12+9х=1
11х=1-12
11х= -11
х= -1
у= -4-3х
у= -4-3*(-1)
у= -4+3
у= -1
Решение системы уравнений (-1; -1).
2)Решить систему уравнений графически:
2х-у=5
х+3у=6
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Прежде преобразуем уравнения в более удобный для вычислений вид:
2х-у=5 х+3у=6
-у=5-2х 3у=6-х
у=2х-5 у=(6-х)/3
Таблицы:
х -1 0 1 х -3 0 3
у -7 -5 -3 у 3 2 1
Координаты точки пересечения графиков функций (3; 1).
Решение системы уравнений (3; 1).
