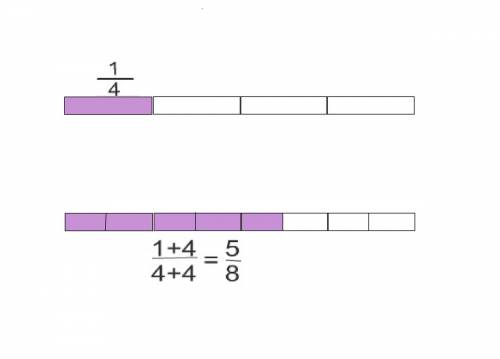
С увеличением числителя и знаменателя на одно и тоже число дробь увеличивается, если она правильная, и уменьшается, если она неправильная
Как это выглядит на примере, смотрите на приложенном рисунке.
То-есть, увеличится количество долей (числитель), но сами эти доли ( каждая) уменьшатся в правильной дроби.
Дробь не меняется, если её и числитель, и знаменатель умножить или разделить на одно и то же число. То-есть увеличить или уменьшить в одинаковое количество раз.
О дробях и не только можно почитать в учебнике и на образовательны сайтах.
При сравнении дробей надо руководствоваться следующими правилами.
Если у дробей одинаковые знаменатели, большей дробью будет та, у которой числитель больше.
Если у дробей одинаковые числители, то большей дробью будет та, у которой знаменатель меньше.
1 Действие.
Сначала сделаем так, чтобы в каждом неравенстве с одной стороны были известные слагаемые, а с другой стороны неизвестные. Для этого переносим с противоположным знаком, 5х-2х больше 1+2
2х+3х меньше 18-3
Получаем: 3х больше 3
5х меньше 15
2 Действие.
Делим левую и правую часть первого неравенства на 3: х больше 1
Делим левую и правую часть второго неравенства на 5: х меньше 3
3 Действие.
Записываем эти два неваренства в виде одного ДВОЙНОГО НЕРАВЕНСТВА:
1 меньше Х меньше 3.
4 Действие. Запишем ответ в виде промежутка: Х ( 1; 3; )
ОТВЕТ: Х принадлежит от 1 до 3 не включительно.
1) (10,5 - 11,8) * 20 и 40/49 * 9,4 - 34
-1,3 * 20 и 40*94/49*10 - 34
-26 и 376/49 - 34
-26 и 376-1666 / 49
-26 и -1290/49
-26 > -26 16/49
2) 7,4 * 15/37 + 19 и (-2,97 + 3,07) - 8,9
74*15 / 37*10 + 19 и 0,1 - 8,9
3 + 19 и -8,8
22 > -8,8