Все задачи на движение требуют для начала вспомнить основную формулу, связывающую скорость, путь и время:
V=S/t/
Задачи на движение по реке чаще всего содержат в себе:
Моторные лодки или катера, обладающие собственным двигателем или судна которые плывут с ручной гребли.
Плот или иные судна, которые могут плыть ТОЛЬКО по течению и со скоростью, равной скорости течения.
Также в таких задачах всегда следует учитывать, что при движении по течению к собственной скорости судна прибавляется скорость течения. А когда движение происходит против течения, наоборот, из собственной скорости судна следует ВЫЧЕСТЬ скорость течения.
Учитывая все выше изложенное составим уравнение для задачи:
Время на весь путь 14 часов.
ВРЕМЯ движения по теч-ю ПЛЮС ВРЕМЯ движ-я против течения = 14ч.
Из основной формулы выразим ВРЕМЯ (t).
t=S/V
t(по теч)=S(по теч) / V(по теч)
t(прот теч)=S(прот теч) / V(прот теч)Пусть х собственная скорость,
тогда (х+2) км/ч скорость по течению реки, а (х-2) км/ч скорость против течения.
Получим
45/(х+2)+45/(х-2)=14
45х-90+45х+90=14х²-56
90х=14х²-56
14х²-90х-56=0
7х²-45х-28=0
D=2025-4*7*(-28)=2809
х=(45+53)/14=7 км/ч собственная скорость спортивной лодки
ответ:7 км/ч
и 
Объяснение:
Первый модуль обращается в ноль при x=-2, второй - при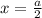 
.
Пусть сначала
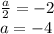
Тогда уравнение принимает вид 
и, очевидно, не имеет решений.
Пусть теперь
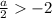
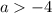
Если 
, то оба модуля раскрываются с плюсом и уравнение принимает вид:
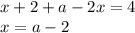
Полученный x будет корнем уравнения, если он принадлежит рассматриваемому отрезку, то есть если 
удовлетворяет системе неравенств
Решение системы: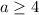 
Если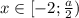 
, то уравнение принимает вид
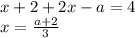
Полученный x будет корнем уравнения, если удовлетворяет системе:
Решение системы: 
Пусть, наконец,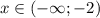 
. Тогда уравнение принимает вид
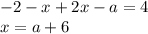
Полученный x будет корнем уравнения, если удовлетворяет системе:
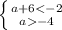
Эта система не имеет решений.
Теперь пусть 
, то есть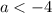 
.
Если 
, то
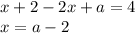
Система:
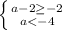
Нет решений.
Если 
, то
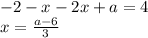
Система:
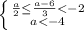
Решение системы: 
И наконец, если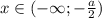 
, то
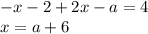
Система:
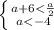
Решение: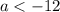 
Из вышесказанного очевидно, что
При 
- два решения
При - одно решение
При 
- нет решений
При 
- нет решений
При - одно решение
При 
- два решения
Таким образом, уравнение имеет одно решение при и
Нет Не имеет 2 корня.