2 задача
Объяснение:
1) Выясним какой возраст у папы, если известно, что ему в 2 раза меньше лет, чем дедушке, а общий их возраст составляет 111 лет. Составляем уравнение по условию задачи, где:
Х - лет папе;
2Х - лет дедушке;
111 - лет общий возраст.
Х + 2Х = 111;
3Х = 111;
Х = 111 / 3;
Х = 37 лет.
2) Выясним какого возраста дедушка, если известно, что он в 2 раза старше папы.
37 * 2 = 74 года.
ответ: возраст папы 37 лет, а возраст дедушки составил 74 года.
1 задача Число деталей, произведенных первым и вторым рабочими, обозначим с условных переменных "Х" и "У" соответственно.
На следующим этапе получим уравнения:
1) Х + У = 657;
2) Х - У = 63.
В итоге решения этих уравнений получаем Х = 63 + У.
Подставив Х в первое уравнение, имеем 63 + У + У = 657 или 2У = 657 - 63 или 2У = 594 или У = 594 / 2 = 297 деталей.
Следовательно, Х будет равен 63 + 297 = 360 деталей.
ответ: 1-ый рабочий - 360 деталей, 2-ой рабочий - 297 деталей
Объяснение:
10.
b₄=6 b₉-192 S₅=?
{b₄=b₁*q³=6
{b₉=b₁q⁸=192
Разделим второе уравнение на первое:
q⁵=32
q⁵=2⁵
q=2 ₁
b₄=b₁q³=6
b₁*2²=6
8*b₁=6 |÷8
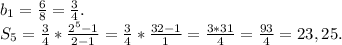
ответ: S₅=23,25.
11.
Принимаем поле за единицу (1).
Пусть скорость вспашки первого тракториста - х, а второго - у. ⇒
{1/(x+y)=6 {6*(x+y)=1 {6x+6y=1 |×2 {12x+12y=2
{4*x+9*y=1 {4x+9y=1 {4x+9y=1 |×3 {12x+27y=3
Вычитаем из второго уравнения первое:
15y=1 |÷15
y=1/15. ⇒
6x+6*(1/15)=1
6x+(6/15)=1
6x+(2/5)=1
6x=3/5 |÷6
x=1/10. ⇒
Время, за которое может вспахать поле первый тракторист, работая один, равно: 1/(1/10)=10 (час).
Время, за которое может вспахать поле второй тракторист, работая один, равно: 1/(1/15)=15 (час).