не уверен шо правельно но
обоих случаях у нас квадратная функция, значит, это графики парабол. Для их построения необходимо минимум 3 точки, одна из которых - это вершина параболы.
Вершина параболы имеет какие-то координаты (х;y).
Вершину можно найти по формуле х = - b/2a
Для случая а) а =1, b = -2, c = -8. Получаем координату х = 1. Подставляем щначение х в искомое выражение и получаем координаты вершины параболы (1; -9)
Для случая б) а = -1, b = 5, c = 0. Получаем координату х = 2.5. Подставляем щначение х в искомое выражение и получаем координаты вершины параболы (2.5; 5)
Теперь берём произвольное значение x и подставляем в функцию, таким образом получаем искомые графики.
На остальные вопросы легко ответить, смотря на график.

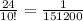

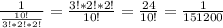
Пишите задание понятно и исчерпывающе!
f(x)=корень(x^2-2x)
f'(x)=(корень(x^2-2x))'=1/(2*корень(x^2-2x)) *(x^2-2x)'=(2x-2)/(2*корень(x^2-2x))=
=(x-1)/корень(x^2-2x)
f'(3)=(3-1)/корень(3^2-3)=2/корень(6)=2*корень(6)/6=корень(6)/6
f(x)=корень(x^2+1)
f'(x)=(корень(x^2+1))'=1/(2*корень(x^2+1))' *(x^2+1)'=2x / (2*корень(x^2+1))=
=x/корень(x^2+1)
f'(2)=2/корень(2^2+1)=2/корень(5)=2/5*корень(5)
f(x)=(x^2+1)*под корнем x^2+1=(x^2+1)^(3/2)
f'(x)=( (x^2+1)^(3/2) )'=3/2 *(x^2+1)^(3/2-1) * (x^2+1)'=3/2 *корень(x^2+1)* 2x=
=3x*корень(x^2+1)
f'(корень(3))=3*корень(3) *корень((корень(3))^2+1)=
=3*корень(3)*2=6*корень(3)
Подробнее - на -