сократи степени и готово
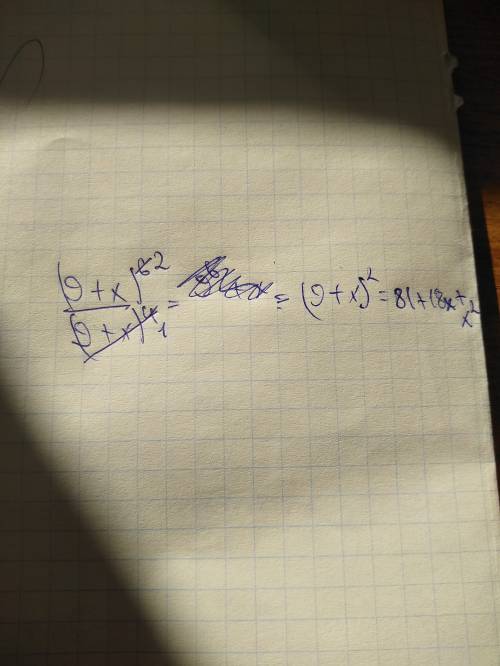
Если a∈(0;1|, то 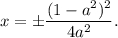 При прочих a решений нет.
При прочих a решений нет.
Объяснение:
Поскольку 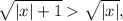 делаем вывод, что a>0. Кроме того, функция
делаем вывод, что a>0. Кроме того, функция 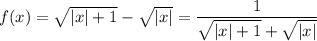 четная (f(-x)=f(x)) и при x>0 убывающая. Поэтому самое большое значение эта функция достигает при x=0, и это значение равно 1. Поэтому для a можно сделать и такое ограничение: a≤1. Пока мы не знаем, как эти рассуждения нам жить, но хуже точно не будет. Итак, a∈(0;1].
четная (f(-x)=f(x)) и при x>0 убывающая. Поэтому самое большое значение эта функция достигает при x=0, и это значение равно 1. Поэтому для a можно сделать и такое ограничение: a≤1. Пока мы не знаем, как эти рассуждения нам жить, но хуже точно не будет. Итак, a∈(0;1].
Обозначим:
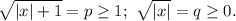 Заметим, что
Заметим, что
p²-q²=|x|+1-|x|=1, поэтому для нахождения p и q имеем систему
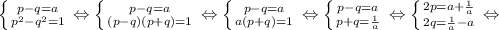
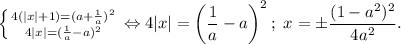
Кстати, то, что a∈ (0;1), мы использовали при возведении в квадрат второго уравнения системы.
Функция 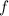 называется парной, если:
называется парной, если:
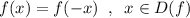
Учитывая это попробуем узнать, могут ли выполняться равенства:
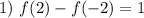
Поскольку по условию функция 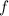 парная, то:
парная, то:
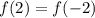
Любое число минус это же число = 0. Значит равенство 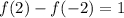 выполняться не может. Можно это доказать. Пусть
выполняться не может. Можно это доказать. Пусть 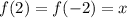 , тогда:
, тогда:
 - не верно. Следовательно, уравнение не имеет корней и
- не верно. Следовательно, уравнение не имеет корней и 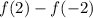 не может быть равно единице.
не может быть равно единице.
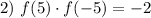
Поскольку по условию функция 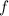 парная, то:
парная, то:
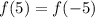
При умножении двух равных чисел не может получиться отрицательное число. Потому что при умножении положительных чисел получается положительное число, и при умножении отрицательных чисел также получается положительное число. То есть:
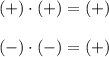
Значит равенство 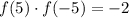 выполняться не может (поскольку -2 -- отрицательное число). Это можно доказать. Пусть
выполняться не может (поскольку -2 -- отрицательное число). Это можно доказать. Пусть 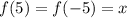 , тогда
, тогда 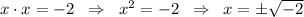 корня квадратного из отрицательного числа не существует. Следовательно уравнение не имеет решений и
корня квадратного из отрицательного числа не существует. Следовательно уравнение не имеет решений и 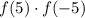 не может быть равно -2.
не может быть равно -2.
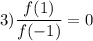
Поскольку по условию функция 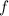 парная, то:
парная, то:
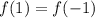
При делении равных чисел результат всегда равен 1. Значит равенство 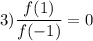 выполняться не может. Доказательство:
выполняться не может. Доказательство:
Пусть 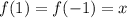 , тогда
, тогда 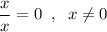 . Домножим обе части уравнения на x, тогда
. Домножим обе части уравнения на x, тогда 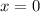 , что не удовлетворяет ОДЗ. Значит уравнение не имеет корней и
, что не удовлетворяет ОДЗ. Значит уравнение не имеет корней и 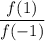 не может быть равно 0.
не может быть равно 0.
(9+x)^6:(9+x)^4=(9+x)^2. ответ: (9+x)^2. ^- это степень.