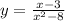
1) 
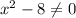
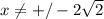
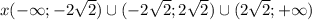
2) 
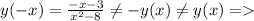не является четной и нечетной
3)Горизонтальная:
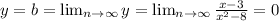
y=0 - горизонтальная асимптота
Наклонная: y=kx+b
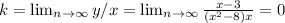
Наклонных нет
Вертикальная x = a, где а - точка разрыва
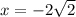
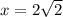- вертикальные асимптоты
4) 
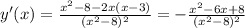
y' не сущ. при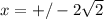 
y' = 0 при х=2; х=4
- - + + -
-----------0-----------------.-----0---------.----------->x
-2sqrt(2) 2 2sqrt(2) 4
x = 2 - точка min y(2) = 1/4 - наименьшее значение
x = 4 - точка max y(4) = 1/8 - наибольшее значение
5)OX: y=0; x = 3 A(3;0)
OY: x=0; y=3/8 B(0;3/8)
ответ:
данные решаются по одному алгоритму.
продемонстрируем на примере первой функции (вторая исследуется аналогично, только функция не определена в точке х=4):
1)
функция не определена в точке x = - 4.
поэтому:
x ∈ (-∞; -4) ∪ (-4; +∞)
2)
находим производную функции:
y'(x) = [(x²+3x)'·(x+4)-(x²+3x)·(x+4)'] / (x+4)²
y'(x) = [(2x+3)·(x+4)-(x²+3x)·1] / (x+4)²
y'(x) = (x²+8x+12) / (x+4)²
3)
приравняем производную к нулю:
x²+8x+12 = 0
x₁ = - 6
x₂ = -2
4)
на интервале x∈(-∞; -6)
y'(x) > 0; функция монотонно возрастает.
на интервале x∈(-6; -4)
y'(x) < 0; функция монотонно убывает.
в точке x = -6 - максимум функции.
y(-6) = - 9
5)
на интервале x∈( -4; -2)
y'(x) < 0; функция монотонно убывает .
на интервале x∈(-2; +∞)
y'(x) > 0; функция монотонно возрастает.
в точке x = - 2 - минимум функции.
y(-2) = -1
6)
для контроля строим график
объяснение:
2a)
- 2(2b - 3) + 4(3b - 2) = - 4b + 6 + 12b - 8 = 8b - 2
б)
15a - (a + 3) + (2a - 1)= 15a - a - 3 + 2a - 1 = 16a - 4
в)
5a - (6a - (7a - (8a - 9))) = 5a - (6a - (7a - 8a + 9)) = 5a - (6a + a - 9) = 5a - (7a - 9)=
= 5a - 7a + 9 = 9 - 2a
3)
- 2(3,5y - 2,5) + 4,5y - 1 = - 7y + 5 + 4,5y - 1 = - 2,5y + 4
- 2,5 * 4/5 + 4 = - 2 + 4 = 2