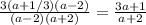
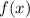Алгебра: Найти сумму целых решений , удовлетворяющих условию

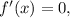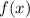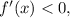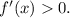
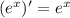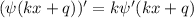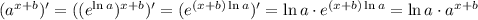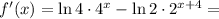
Для поиска наименьшего значения функции необходимо найти ноли производной т.е. точки, где у функции будет экстремум, и показать, что до экстремума функция падает, т.е. производная а после экстремума функция растёт, т.е. производная 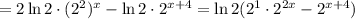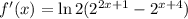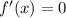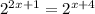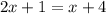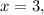Пользуемся правилами дифференцирования: 1) ; 2) ; 3) ; Берём производную, в соответствии с 3) : ; ; Потребуем: ; ; ; ; причём это единственный корень. При например при 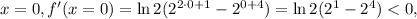т.е. функция убывает. 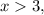При например при 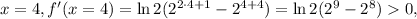т.е. функция растёт. 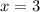Значит при как раз достигается минимум:...

Найти сумму целых решений , удовлетворяющих условию

👇

Увидеть ответ

Ответ:

ТуристАртемий

19.07.2020

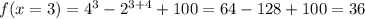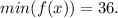
Необязательно решать неравенство, чтобы ответить на вопрос задачи.

Преобразуем неравенство к виду:

$(7^{x+3}-7^{2x+2})+(2^{x+3}-2^{2x+5})0$

Когда неравенство выполнится? Когда два слагаемых будут точно положительны, а это происходит, если вычитаемое в каждой скобке меньше соответствующего уменьшаемого. То есть справедлива следующая система неравенств:

$\left \{ {{7^{x+3}7^{2x+2}} \atop {2^{x+3}2^{2x+5}}} \right.\\\left \{ {{x+32x+2} \atop {x+32x+5}} \right.\Leftrightarrow x+32x+5 \Rightarrow x$

Значит, все x ∈ [-5; -2) нам точно подходят.

Теперь рассмотрим случай, когда неравенство точно не выполнится. Это случай, противоположный первому.

$\left \{ {{x+3$

Значит, все x ∈ (1; 5] нам точно не подходят.

Остаётся перебрать оставшиеся x: -2; -1; 0; 1.

При x = -2 получаем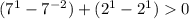 $(7^1-7^{-2})+(2^1-2^1)0$

При x = -1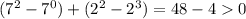 (7^2-7^0)+(2^2-2^3)=48-40

При x = 0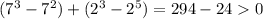 (7^3-7^2)+(2^3-2^5)=294-240

При x = 1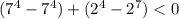 (7^4-7^4)+(2^4-2^7) - не удовлетворяет условию

Следовательно, нужные нам x: -5, -4, -3, -2, -1, 0. Их сумма равна -15.

ответ: -15

4,4(56 оценок)

Открыть все ответы

Ответ:

рамзан010191271894

19.07.2020

1)
(х-5) / (х+6) >0
+ +
------o-------o------>x
-6 - 5
ответ: x∈(-∞; -6)U(5; +∞)

2)
3a2-5a-2 = 0
D=25+24=49
a(1)=(5+7) / 6 = 2
a(2)=(5-7) / 6 = -1/3

дробь = $\frac{3(a+1/3)(a-2)}{(a-2)(a+2)} = \frac{3a+1}{a+2}$

3)...
Система
у=8-х
х2+(8-х)2 = 80

х2+64-16х+х2 -80=0
2х2-16х-16=0
х2-8х-8=0
Д=64+32=96
х(1; 2)=(8+-√96)/2 = (8+-4√6)/2 = 4+-2√6
х(1) = 4+2√6 у(1) = 8-(4+2√6) = 4-2√6
х(2) = 4-2√6 у(2) = 8-(4-2√6) = 4+2√6

4)
у=х2+6х+17+с
Одна общая точка с осью ОХ, это значит один нуль функции, значит один корень уравнения х2+6х+17+с=0, а это значит, что Д=0
Д=36-4(17+с) = 36-68-4с = -32-4с
-32-4с =0
4с=-32 | :4
c=-8 при этом исходная функция имеет только одну общую точку с осью Ох.

у=х2+6х+9

График - парабола, ветви вверх
Найдем вершину В(х;у)
х(в) = -6/2 = -3
у(в) = 9-18+9=0
В(-3;0) - вершина - единственный ноль функции

Чертим систему координат, стрелками отмечаем положительное направление , подписываем оси (х - вправо и у- вверх), отмечаем начало координат - точку О и отмечаем единичные отрезки по обеим осям. Отмечаем точку В в этой системе координат;
далее пунктиром чертим новую систему координат относительно точки В и этой "новой системе координат" строим по точкам параболу у=х2.

х=0 1 -1 2 -2 1/2 -1/2
у=0 1 1 4 4 1/4 -1/4

Соединяем плавной линией точки, подписываем график. Всё!

4,6(57 оценок)

Ответ:

max50chepil

19.07.2020

Для поиска наименьшего значения функции f(x)

необходимо найти ноли производной f'(x) = 0 ,

т.е. точки, где у функции будет экстремум, и показать, что до экстремума функция f(x)

падает, т.е. производная f'(x) < 0 ,

а после экстремума функция растёт, т.е. производная f'(x) 0 .

Пользуемся правилами дифференцирования:

1) ( e^x )' = e^x

;

2) $( \psi (kx+q) )' = k \psi '(kx+q)$ ;

3) $( a^{x+b} )' = ( ( e^{ \ln{a} } )^{x+b} )' = ( e^{ (x+b) \ln{a} } )' = \ln{a} \cdot e^{ (x+b) \ln{a} } = \ln{a} \cdot a^{x+b}$ ;

Берём производную, в соответствии с 3) :

$f'(x) = \ln{4} \cdot 4^x - \ln{2} \cdot 2^{x+4} =$

$= 2\ln{2} \cdot (2^2)^x - \ln{2} \cdot 2^{x+4} = \ln{2} ( 2^1 \cdot 2^{2x} - 2^{x+4} )$ ;

$f'(x) = \ln{2} ( 2^{2x+1} - 2^{x+4} )$ ;

Потребуем: f'(x) = 0