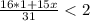
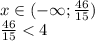При каких значениях параметра a уравнение |x^2-2ax|=a имеет три различных действительных корня?

Question

Алгебра: При каких значениях параметра a уравнение |x^2-2ax|=a имеет три различных действительных корня?

kauymbek · Accepted Answer

1) Оценим сумму , для этого примем что есть равные числа. Так как есть место для чисел 3 4 и 6 это 3 числа.
$\frac{16*1+15x}{31}$
$x \in (-\infty;\frac{46}{15})\\ \frac{46}{15}$ то есть да может , так как 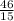$\frac{46}{15}$ ее целая часть равна 3 , а она натуральное число , и найдется набор таких чисел что среднее арифметическое будет меньше 2 , так как в условий не сказано что , сам набор может состоят так только из разных натуральных чисел.
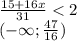2) $\frac{15+16x}{31}$ , целая часть этого числа равна

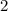, то есть не может , так как в сумме 2=1+1

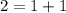, и по количеству в этом наборе минимальное есть 16 единиц .
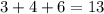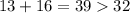3) $3+4+6=13\\$ так как мы ранее доказали что , есть не менее 16 единиц , и того 13+16=3932

что удовлетворяет условию .

MOGZ ответил