Вхудожественных произведениях может присутствовать пунктуация.

👇

Ответ:

aushatsy

12.11.2022

В художественных произведениях может присутствовать авторская пунктуация.

Под авторской пунктуацией имеется в виду манера автора расставлять знаки препинания. Читая разные художественные тексты, мы можем обратить внимание на некоторые отступления от общих правил пунктуации. Некоторые писатели увлекаются многоточиями, а другие часто используют тире. Своеобразная манера расстановки знаков препинания становится "визитной карточкой" писателя. Например, Ф. М. Достоевский любил использовать тире после союза и, а тексты Максима Горького - "чемпионы" по количеству тире.

4,4(19 оценок)

Открыть все ответы

Ответ:

kkalipso

12.11.2022

Рост у Алисы сравнительно невысокий – где-то 160 см, и то в сапогах на толстой подошве. У Алисы невероятные рыжие волосы, в существование которых трудно поверить – такого натурального, морковно-ораьнжвого цвета Волос Алиса больше нигде не видела. У девочки большие, зеленые, как изумруд глаза и пухлые щеки – результат бесконечного поедания сладостей. Фигура у Алиса отнюдь не модельная – она выделятся из общей массы тонких и худых одноклассниц. Нельзя сказать, что Алиса толстая, но говорить о том, что она уж больно худая тоже не полагается. Впрочем, на руки ее подхватить весьма легко. У Алисы всегда веселый и жизнерадостный взгляд, глаза ее всегда горят огнем предвкушения какого-то великого открытия, потому что каждый раз, открывая глаза, Алиса верит, что вот-вот разглядит где-то вдалеке белого кролика. Алиса предпочитает носить одежду средневекового стиля, что подчеркивает ее индивидуальность. Помимо всего этого в гардеробе Алисы нету ни одной пары брюк – она носит исключительно юбки, платья и сарафаны, что тоже является частью ее странного образа девочки из Страны чудес.
Когда Алиса говорит она внимательно смотрит в глаза своего собеседника – девочка уверена, глаза всегда говорят куда больше слов. Для нее глаза – самое важное в человеке.
Кожа у Алисы светлая, как и у любого человека, который рос в дождливом и пасмурном Лондоне.
И еще пару слов о очень-очень рыжих Алисиных волосах - это ее главная гордость. Когда-то она вбила себе в голову что рыжий цвет волос - самый волшебный.

4,6(52 оценок)

Ответ:

arinasuykova

12.11.2022

Вообще область значений тангенса и котангенса - все действительные числа:

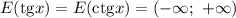
$E(\mathrm{tg}x)=E(\mathrm{ctg}x)=(-\infty;\ +\infty)$

а)

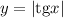
$y=|\mathrm{tg}x|$

Если рассмотреть модуль тангенса, то отрицательные значения примут противоположные значения, то есть станут положительными. Нулевое и положительные значения сохранятся. Получим область значений:

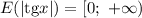
$E(|\mathrm{tg}x|)=[0;\ +\infty)$

б)

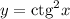
$y=\mathrm{ctg}^2x$

Котангенс может принять значение любого действительного числа, но при возведении любого числа в квадрат результат получится неотрицательным.

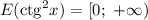
$E(\mathrm{ctg}^2x)=[0;\ +\infty)$

в)

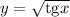
$y=\sqrt{\mathrm{tg}x}$

Тангенс может принять значение любого действительного числа. Под знак корня из них можно записать любое неотрицательное, при этом в результате может получиться любое неотрицательное число.

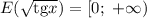
$E(\sqrt{\mathrm{tg}x})=[0;\ +\infty)$

г)

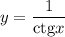
$y=\dfrac{1}{\mathrm{ctg}x}$

Котангенс может принять значение любого действительного числа. При делении 1 на любое число (отличное от нуля) может получиться любое число, кроме нуля.

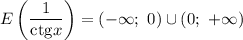
$E\left(\dfrac{1}{\mathrm{ctg}x}\right)=(-\infty;\ 0)\cup(0;\ +\infty)$