Алгебра: Решить уравнение: (а-2)х+2=2 при х=0 и х не равно 0 20

Решить уравнение: (а-2)х+2=2 при х=0 и х не равно 0 20

👇

Увидеть ответ

Ответ:

temik25527

13.06.2020

Найдём значение параметра а при значениях х=0 и х=/0.

запишем уравнение в виде

(а-2)х=0

1) х =0; а €R (всем действительным числам) ;

2) х=/0; тогда а-2=0/х; а=2

4,4(61 оценок)

Ответ:

kocmoc505

13.06.2020

Вообще это уравнение с параметром, и нужно подставлять 0 не в искомое, а в параметр, в данном случае - а.

1) если а-2=0

0*х=0

х-любое

2) если а-2 не равно 0

х=0/(а-2)=0

4,8(5 оценок)

Открыть все ответы

Ответ:

simpolita

13.06.2020

Если функция имеет вид y=2x^3+9x^2-18x+15, то вот её график:

Область определения функции. ОДЗ: -00<x<+00
Точка пересечения графика функции с осью координат Y:График пересекает ось Y, когда x равняется 0: подставляем x=0 в 2*x^3+9*x^2-18*x+15.
Результат: y=15. Точка: (0, 15)Точки пересечения графика функции с осью координат X:График функции пересекает ось X при y=0, значит нам надо решить уравнение:2*x^3+9*x^2-18*x+15 = 0Решаем это уравнение и его корни будут точками пересечения с X:
x=-(3*sqrt(85)/4 + 111/8)**(1/3) - 21/(4*(3*sqrt(85)/4 + 111/8)**(1/3)) - 3/2. Точка: (-(3*sqrt(85)/4 + 111/8)**(1/3) - 21/(4*(3*sqrt(85)/4 + 111/8)**(1/3)) - 3/2, 0)Экстремумы функции:Для того, чтобы найти экстремумы, нужно решить уравнение y'=0 (производная равна нулю), и корни этого уравнения будут экстремумами данной функции:
y'=6*x^2 + 18*x - 18=0
Решаем это уравнение и его корни будут экстремумами:
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=18^2-4*6*(-18)=324-4*6*(-18)=324-24*(-18)=324-(-24*18)=324-(-432)=324+432=756;
Дискриминант больше 0, уравнение имеет 2 корня:x_1=(2root756-18)/(2*6)=(2root756-18)/12=2root756/12-18/12=2root756/12-1.5 ≈ 0.79128784747792;
x_2=(-2root756-18)/(2*6)=(-2root756-18)/12=-2root756/12-18/12=-2root756/12-1.5 ≈ -3.79128784747792.x=-3/2 + sqrt(21)/2. Точка: (-3/2 + sqrt(21)/2, -9*sqrt(21) + 2*(-3/2 + sqrt(21)/2)^3 + 9*(-3/2 + sqrt(21)/2)^2 + 42)x=-sqrt(21)/2 - 3/2. Точка: (-sqrt(21)/2 - 3/2, 2*(-sqrt(21)/2 - 3/2)^3 + 9*sqrt(21) + 42 + 9*(-sqrt(21)/2 - 3/2)^2)Интервалы возрастания и убывания функции:Найдем интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим на ведет себя функция в экстремумах при малейшем отклонении от экстремума:Минимумы функции в точках:-3/2 + sqrt(21)/2Максимумы функции в точках:-sqrt(21)/2 - 3/2Возрастает на промежутках: (-oo, -sqrt(21)/2 - 3/2] U [-3/2 + sqrt(21)/2, oo)Убывает на промежутках: [-sqrt(21)/2 - 3/2, -3/2 + sqrt(21)/2]Точки перегибов графика функции:Найдем точки перегибов для функции, для этого надо решить уравнение y''=0 - вторая производная равняется нулю, корни полученного уравнения будут точками перегибов указанного графика функции,
+ нужно подсчитать пределы y'' при аргументе, стремящемся к точкам неопределенности функции:y''=12*x + 18=0
Решаем это уравнение и его корни будут точками, где у графика перегибы:x=-3/2. Точка: (-3/2, 111/2)Интервалы выпуклости, вогнутости:Найдем интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках изгибов:Вогнутая на промежутках: [-3/2, oo)Выпуклая на промежутках: (-oo, -3/2]Вертикальные асимптоты графика функции:Горизонтальную асимптоту найдем с предела данной функции при x->+oo и x->-oo. Соотвествующие пределы находим :lim 2*x^3+9*x^2-18*x+15, x->+oo = oo, значит горизонтальной асимптоты справа не существуетlim 2*x^3+9*x^2-18*x+15, x->-oo = -oo, значит горизонтальной асимптоты слева не существуетНаклонные асимптоты графика функции:Наклонную асимптоту можно найти, подсчитав предел данной функции, деленной на x при x->+oo и x->-oo. Находим пределы :lim 2*x^3+9*x^2-18*x+15/x, x->+oo = oo, значит наклонной асимптоты справа не существуетlim 2*x^3+9*x^2-18*x+15/x, x->-oo = oo, значит наклонной асимптоты слева не существуетЧетность и нечетность функции:Проверим функци четна или нечетна с соотношений f(x)=f(-x) и f(x)=-f(x). Итак, проверяем:2*x^3+9*x^2-18*x+15 = -2*x^3 + 9*x^2 + 18*x + 15 - Нет2*x^3+9*x^2-18*x+15 = -(-2*x^3 + 9*x^2 + 18*x + 15) - Нетзначит, функция не является ни четной ни нечетной

4,6(43 оценок)

Ответ:

nkartalev

13.06.2020

Отрезки МН и РО пересекаются в их середине К. Докажите, что МР параллелен НО.

========================================================

▪Первый МРК = ΔОКН по двум сторонам и углу между ними:МК = КН , РК = КО - по условию∠MKP = ∠OKH - как вертикальные углыВ равных треугольниках соответственно равные элементы: стороны и углы ⇒ ∠РМК = ∠ОНК , ∠МРК = ∠НОК - как накрест лежащие углы. Значит, МР || НО , что и требовалось доказать.▪Второй Рассмотрим четырёхугольник ОМРН:Диагонали данного четырёхугольника точкой пересечения делятся пополам ( признак параллелограмма ). Из этого следует, что ОМРН - параллелограмм ⇒ МР || НО , что и требовалось доказать.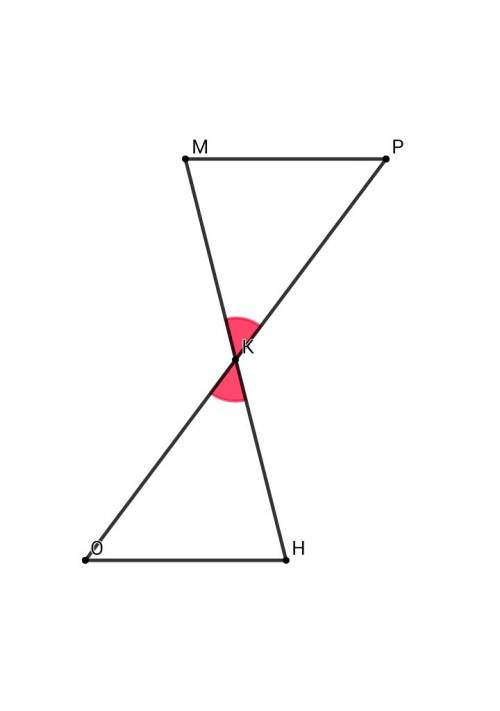
Отрезки мн и ро пересекаются в их середине к.докажите, что мр параллелен но.