1)Задание
Интервал (часы) 0-1 1-2 2-3 3-4
Частота 3 9 12 6
30-100% х=(6*100)/30
6-х% х=20%- выполняют домашнее более трех частот
2)Задание
а)2016
б)20%
3)Задание
СОРИ НЕ ЗНАЮ
4)Задание
Определим моменты времени, когда камень находился на высоте ровно 9 метров. Для этого решим уравнение h(t)=9:
Проанализируем полученный результат: поскольку по условию задачи камень брошен снизу вверх, это означает, что в момент времени t=0,6(с) камень находился на высоте 9 метров, двигаясь снизу вверх, а в момент времени t=3(с) камень находился на этой высоте, двигаясь сверху вниз. Поэтому он находился на высоте не менее девяти метров 2,4 секунды.
ответ: 2,4.
5)Задание
Пусть х- скорость лодки в стоячей воде;
тогда х-2 и х+2 скорость лодки соответственно против течения и по течению
8/(x-2) время против течения
12/(x+2)-время по течению
в сумме по условию это составило 2 часа
8/(x-2)+12/(x+2)=2
4/(x-2)+6/(x+2)=1
(4x+8+6x-12)=x^2-4
10x-4=x^2-4
x=10
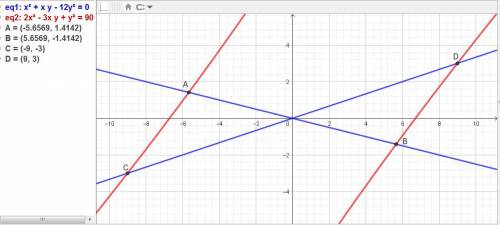
Дана система уравнений:
{x²+xy-12y²=0
{2x²-3xy+y²=90.
Первое уравнение представим так:
x²- (3xy + 4xy) + (-3y*4y) = 0.
Это равносильно разложению на множители:
(x - 3y)(x + 4y) = 0.
Отсюда выразим у = х/3 и у = -х/4, которые подставим во второе уравнение.
Подставим у = х/3.
2x² - 3x(х/3) + (х/3)² = 90,
2x²- x²+ (x²/9)=90,
10x²= 9*90
x = ± 9.
y = ± 9/3 = ± 3.
Найдены 2 корня: х1 = -9, у1 = -3, х2 = 9, у2 = 3.
Подставим у = -х/4.
2x² - 3x(-х/4) + (-x/4)² = 90,
2x²+ (3x²/4)+ (x²/16)=90,
32x² + 12x² + x²= 16*90.
45x²= 16*90
x = √32 = ±(4√2).
y = ± (4√2/4) = ± √2.
Найдены ещё 2 корня: х3 = -(4√2), у1 = √2, х4 = (4√2), у4 = -√2.
ответ: х1 = -9, у1 = -3, х2 = 9, у2 = 3.
х3 = -(4√2), у1 = √2, х4 = (4√2), у4 = -√2.