500
100/30=3.333
3.33*150=499.55=500
Обозначим Q1 - производительность первой трубы (сколько литров в минуту она пропускает), Q2 - производительность второй трубы
V1-объем 1 резервуара (который заполняет первая труба)
V2 - объем второго резервуара (который заполняет вторая труба)
t1-время за которое первая труба заполнит 1 резервуар
t2- время за которое вторая труба заполнит 2 резервуар
Теперь на основании этого составляем уравнения:
Q1*t1=V1
Q2*t2=V2
Из условий задачи известно, что: Q1=Q2-5
Так же известно, что t2=t1-140 (140 это 2 часа 20 минут в минутах).
Этого достаточно для составления системы уравнений:
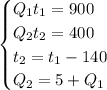
Решаем ее: во второе уравнение подставляем Q1+5 вместо Q2 и t1-140 вместо t2
Получаем следующую систему:
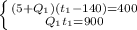
Из второго уравнения выражаем t1, получаем: 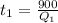
Подставляем в 1 уравнение, получаем:
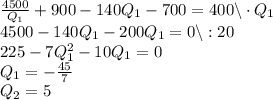
Первый ответ не подходит, потому что он отрицательный, значит берем второй.
Значит первая труба пропускает Q1=5 л/мин
ответ: первая труба пропускает Q1=5 л/мин
Пусть x=производительность(л/мин)1-й трубы тогда(x+5) производительность второй трубы.Первая труба заполняет резервуар в 400 литров за (400/x)Вторая труба заполняет резервуар в 900 литров за (900/x+5))
2 часа 20 мин=140 мин
Уравнение:
400/x-900/(x+5)=140
Делим на 20:
20/x-45/(x+5)=7
200(x+5)-45x=7x(x+5)
20x+100-45x=7x(2)+35x
7x(2)+60x-100=0
D=60(2)+28*100=3600+2800=6400
√D=80
x(1)=(-60+80):14=10/7
x(2)=(-60-80):14=-10(не является решением так как произвдительность не может быть отрицательной)
ответ:10/7 л/мин.
x(2)=(-60-80):14=-10(не является решением т.к.производительность

30/150=0,2 или 20%
ответ: 20%