1) 7x+10=5+12
7x=5+12-10
7x=7
x=7
2)3(2x-5)+5x=7
6x-15+5x=7
11x=22
x=2
3) 5x-3=6(2x+5)+2
5x-3=12x+30+2
5x-12x=30+2+3
-7x=35
x= -5
4)17x-3(5x-4)=8(3x-4)
17x-15x+12=24x-32
2x-24x=-32-12
-22x=-44
x=2
5) 7(4X+5)-4(2+3X)=6x-3
28x+35-8-12x=6x-3
16x+27=6x-3
16x-6x=-3-27
10x=-30
x=-3
6)2,1(2-x)+1,4(1,5x-3)=0
4.2-2.1x+2.1x-4.2=0
0=0
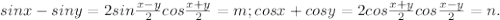
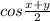 . Выразим его из обоих равенств:
. Выразим его из обоих равенств:
 .
.

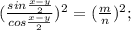
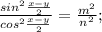
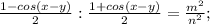
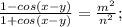
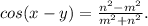

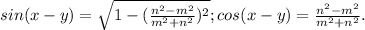
7x=7
x=7:7
x=1
2)6x-15+5x=7
6x+5x=7+15
11x=22
x=22:11
x=2