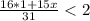
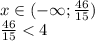то есть да может , так как 
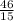ее целая часть равна 3 , а она натуральное число , и найдется набор таких чисел что среднее арифметическое будет меньше 2 , так как в условий не сказано что , сам набор может состоят так только из разных натуральных чисел. 
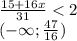, целая часть этого числа равна 
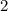, то есть не может , так как в сумме 
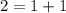, и по количеству в этом наборе минимальное есть 16 единиц . 
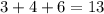так как мы ранее доказали что , есть не менее 16 единиц , и того 
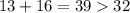что удовлетворяет условию .
Х-(3-х)=2х-а
2х-3=2х-а
3=а
Чтоб уравнение не имело корней, а должно иметь любое значение кроме 3