Пусть за  час 1-й кран будет наполнять весь бассейн
час 1-й кран будет наполнять весь бассейн
за 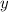 час 2-й кран будет наполнять бассейн.
час 2-й кран будет наполнять бассейн.
Если 1 - это объем всего бассейна, тогда
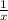 - объем воды, который проходит через 1-й кран за 1 час.
- объем воды, который проходит через 1-й кран за 1 час.
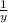 - объем воды, который проходит через 2-й кран за 1 час.
- объем воды, который проходит через 2-й кран за 1 час.
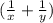 - общая производительность двух кранов.
- общая производительность двух кранов.
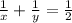 - первое уравнение
- первое уравнение
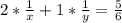 - второе уравнение
- второе уравнение
Из первого уравнения получим: 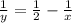 и вставим во второе уравнение:
и вставим во второе уравнение:
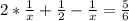
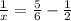
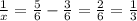
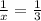
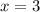
Подставим 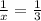 в первое уравнение:
в первое уравнение:
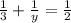
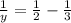

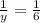
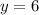
ответ: за 3 часа 1-й кран наполнит весь бассейн;
за 6 часов 2-й кран наполнит весь бассейн.
[1, 1, 1 | 4]
[1, 2, 3 | 7]
[1, 1, 5 | 8]
Умножим первую строку на 1 и прибавим результат к строкам 2 и 3.
[1, 1, 1 | 4]
[0, 1, 2 | 3]
[0, 0, 4 | 4]
Разделим строку 3 на 4:
[1, 1, 1 | 4]
[0, 1, 2 | 3]
[0, 0, 1 | 1]
Умножим строку 3 на 1 и прибавим результат к строке 1:
[1, 1, 0 | 3]
[0, 1, 2 | 3]
[0, 0, 1 | 1]
Умножим строку 3 на 2 и прибавим результат к строке 2:
[1, 1, 0 | 3]
[0, 1, 0 | 1]
[0, 0, 1 | 1]
Умножим строку 2 на 1 и прибавим результат к строке 1:
[1, 0, 0 | 2]
[0, 1, 0 | 1]
[0, 0, 1 | 1]
Преобразуем расширенную матрицу в систему линейных уравнений:
{x = 2
{y = 1
{z = 1
Запишем решение системы:
(2, 1, 1)
ответ: (2, 1, 1).