1. Количество трехзначных чисел, составленных из трех различных цифр из множества цифр 1, 2, 3, 4, 5, 6 и 7, равно количеству размещений без повторения 7 элементов по 3 позициям:
A(7, 3) = 7!/(7 - 3)! = 7!/4! = 7 * 6 * 5 = 210.
2. В общей формуле A(n, m) = n!/(n - m)!, отношение факториалов называется убывающим факториалом. В частном случае, при n = m получим число перестановок n элементов:
A(n, n) = n!/(n - n)! = n!/0! = n!
3. Аналогичный результат получим для размещений n элементов по (n - 1) позициям:
A(n, n - 1) = n!/(n - n + 1)! = n!/1! = n!
ответ. Количество трехзначных чисел: 210
Объяснение:

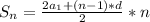


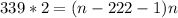
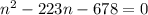

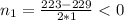
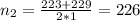
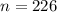
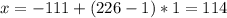
Решение посмотри на фото