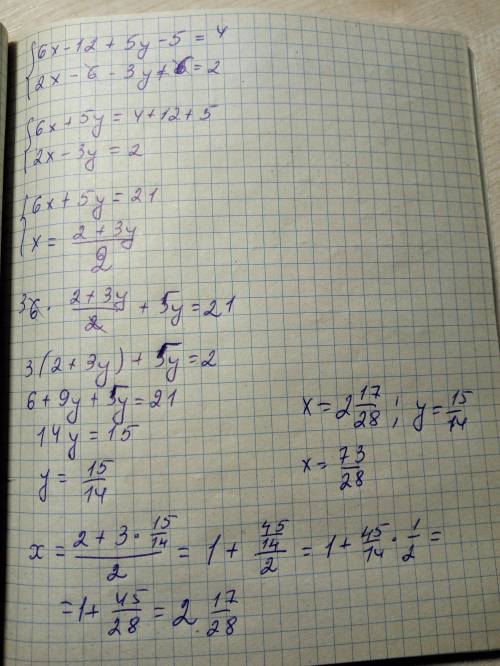
5. Решим квадратное уравнение.
Запишем уравнение в исходном виде:
10х^2 + х - 24 =0
Так как уравнение неприведенное, то решаем через дискриминант:
D = b^2 - 4ac
D = 1 - 4*10*(-24)
D = 1 - (-960) = 1 + 960 = 961
sqrt(D) = sqrt(961) = 31
Находим корни уравнения:
х1 = (-b + sqrt(D))/2a = (-1 + 31)/2*10 = 30/20 = 3/2 = 1,5
х2 = (-b - sqrt(D))/2a = (-1 - 31)/2*10 = -32/20 = -(8/5) = -1,6
ответ: -1,6
6. Вычисляем количество корней уравнения:
ОДЗ: х не равно -2.
х1 = 2
х2 = sqrt(3)
x3 = -sqrt(3)
Следовательно уравнение имеет 3 корня.
Объяснение:
2х-у=2 у=2х-2 у=2х-2
3х+2у=10 ⇔ 3х+2(2х-2)=10 ⇔ 3х+4х-4-10=0 ⇔
у=2х-2 у=2х-2 у=2·2-2=2
7х=14 ⇔ х=2 ⇔ х=2 (2,2)
х-11у=23 х=23+11у х=23+11у
5х+у=3 ⇔ 5(23+11у)+у-3=0 ⇔ 115+55у+у-3=0 ⇔
х=23+11у х=23+11у х=23-22=1
56у=-112 ⇔ у=-2 у=-2 (1,-2)