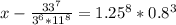
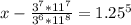
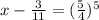
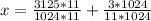
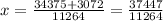
1) f(x) = x^2 - 6x + 5
D(f) = R
1) Знайдемо проміжки монотоності:
f`(x) = 2x - 6 = 2(x - 3)
f`(x) = 0
2(x - 3) = 0
x = 3
(дивись малюнок)
f(x) спадає якщо х ∈ (-∞; 3) і зростає якщо х ∈ (3; +∞)
2) знайдемо точки екстремума.
х(min) = 3 ⇒ y(min) = 3² - 6 * 3 +5 = 9 - 18 + 5 = -4
точки max не існеє.
2) f(x) = x^4 - 2x^2
D(f) = R
1) Знайдемо проміжки монотоності:
f`(x) = 4x³ - 4х = 4х(x² - 1) = 4х(х - 1)(х + 1)
f`(x) = 0
4х(х - 1)(х + 1) = 0
х = 0, х = 1, х = -1
(дивись малюнок)
f(x) спадає якщо х ∈ (-∞; -1) і (0; 1);
зростає якщо х ∈ (-1; 0) і (1; +∞)
2) знайдемо точки екстремума.
х(min) = -1 ⇒ y(min) = (-1)⁴ - 2 * (-1)² = 1 - 2 = -1
х(min) = 1 ⇒ y(min) = 1⁴ - 2 * 1² = 1 - 2 = -1
х(max) = 0 ⇒ y(max) = 0⁴ - 2 * 0² = 0

13) 1
14) 3
15) 4
Объяснение:
Т.к. эти уравнения являются приведенными (коэффициент при х² равен единице), то решаем их по теореме Виета: "Произведение корней приведенного квадратного уравнения равен свободному члену, а сумма корней равна второму коэффициенту, взятому с обратным знаком".
13) x²-6x+5=0
( x₁*x₂=5 и x₁+x₂=6) => x₁=1, x₂=5
x₁=1 < x₂=5
ответ: 1
14) x²-9x+18=0
( x₁*x₂=18 и x₁+x₂=9) => x₁=3, x₂=6
x₁=3 < x₂=6
ответ: 3
15) x²-10x+24=0
( x₁*x₂=24 и x₁+x₂=10) => x₁=4, x₂=6
x₁=4 < x₂=6
ответ: 4