Объяснение:
f(х)=1/3х³+х²-3х+5/3=1/3(х-1)(х+5)
Функция не является ни четной ни нечетной
2, D(f(х)): (-∞;+∞)
Точки пересечения с осями координат
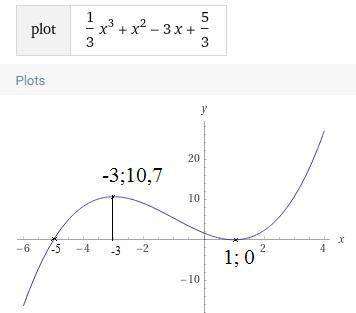
С осью (Ох) А(-5;0) В(1;0)
С осью (Оу) С(0; 5/3)
3. Точки экстремума
Определяем когда f(х) '=0
(1/3х³+х²-3х+5/3)'=0 х²+2х-3=0 Д= D=22- 4·1·(-3)=16
Корни уравнения:
х₁=(-2+4)/(2*1)=1
х₂=(-2-4)/(2*1)=-3
х₁=1 у₁=0
х₂=-3 у₂=10²/₃
4. f(х) возрастает при х∈(-∞;-3)
Убывает х∈(-3;1)
возрастает при х∈(1;+∞)
сводим все в таблицу
х (-∞;-3) -3 (-3;1) 1 (1;+∞)
f(х) ' + 0 - 0 +
f(х) ↑ 10²/₃ ↓ 0 ↑
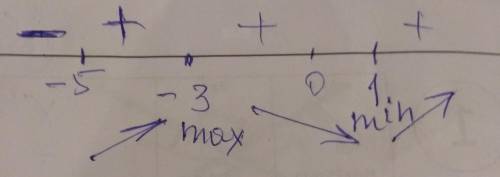
y(x)=-2x-3
y(1)= -2*1-3= -2-3= -5
y(-1)= -2*(-1)-3=2-3= -1
y(0)= -2*0-3= -3
y(0,5)= -2* 0,5-3= -1-3= -4
y(x)=1,приx= -2
y(x)= -1,при х= -1
y(x)= 0,3,при х =1,65
-2x-3<0
-2x<3 ; 2x>-3; x> - 3/2; при x>- 1,5 функция принимает отрицательные значения