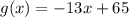. Найдем значение 
, при котором функция будет равна 
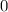. Для этого приравняем саму функцию к :
.
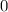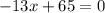
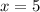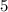данная функция перескает ось абсцисс (OX). Так как у функции угловой коэффициент отрицательный (число -13), следует заключение, что функция убывает на всей области определения. Так как это линейная функция, то область определения у неё, вся числовая прямая. Отсюда следует, что функия - убывающая!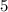. Так как функция убывает, то отсюда получаем:
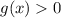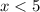
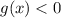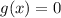при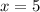 
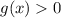при 
.
при 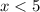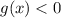при при 
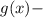убывающая
1) 8*7*6 = 336
2) 20^3 = 8000