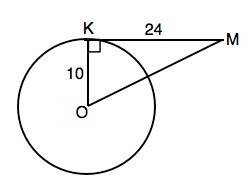
Обозначим центр окружности О, точку касания К.
Радиус, проведенный в точку касания, перпендикулярен касательной. ⇒
∆ МОК - прямоугольный.
Отношение катетов 10:24=5:12 указывает на то, что длины сторон треугольника из Пифагоровых троек 5:12:13, в которых эти длины –целые числа.⇒ МО=2•13=26. И это можно проверить по т.Пифагора.
МО=√(KO²+KM²)=√676=26
В прямоугольном треугольнике каждый катет является высотой, проведенной к другому катету.
Площадь прямоугольного треугольника равна половине произведения катетов:
S=КМ•КО:2=24•10:2=120 см²
линейная ф-ция имеет вид: У=кХ+в, где "к" и "в" - некоторые числа,
причём "к" не равно 0
Задача состоит в том, чтобы найти эти числа к и в.
Т.к. А(4;-5),то Х=4 У=-5
подставим эти значения в линейную ф-цию У=кХ+в
-5=4к+в
так же поступаем с координатами точки В(-2;19) 19=-2к+в
Получили систему двух уравнений с двумя неизвестными,
вычтем из первого ур-я второе:
-5-19=4к-(-2к)+в-в
-24=4к+2к
-24=6к
к=-4
Подставим полученное значение к=-4 в ур-е: -5=4к+в
и найдём "в " -5=4*(-4)+в
в=-5+16
в=11
Подставим полученные к=-4 и в=11 в У=кХ+в
имеем: У=-4Х+11
11/55 можно сократить на 11 и получиться 1/5