![sin [ 4 arccos ( - \frac{1}{2}) - 2 arcctg \frac{ \sqrt{3} }{3} ] = \\ sin [4* \frac{2 \pi }{3} - 2* \frac{ \pi }{3} ] = \\ sin[ \frac{8 \pi }{3} - \frac{2 \pi }{3} ] = sin(2 \pi ) = 0](/tpl/images/0841/6514/75bd3.png)
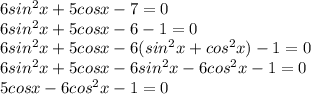
, n,m∈Z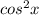
не является корнем ( на ноль делить нельзя), а потом все уравнение почленно разделить на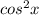 
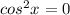
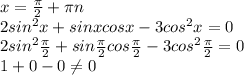
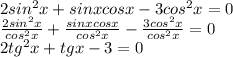
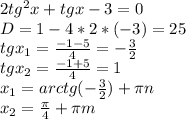
найдем одз. под корнем может находиться только неотрицательное значение, значит 5-х> =0, откуда х< =5. корень может принимать только неотрицательные значения, значит 5-х^2> =0, откуда х^2< =5, откуда |х|< =√5, откуда -√5< =х< =√5.
теперь решение:
вoзведем в квадрат:
(5-x^2)^2=5-x
25-10x^2+x^4=5-x
x^4-10x^2+x+20=0
(x^2-x-4)(x^2+x-5)=0
1) x^2-x-4=0
d=17
x(1)=(1+√17)/2> (1+√16)/2=(1+4)/2=5/2=√5*√5/2> √5*√4/2=√5. значит этот корень не подходит.
x(2)=(1-√17)/2 подставляя в изначальное уравнение, проверяем, что этот корень подходит.
2) x^2+x-5=0
d=21
x(1)=(-1+√21)/2 подставляя в изначальное уравнение, проверяем, что этот корень подходит.
x(2)=(-1-√21)/2< (-1-√16)/2=-5/2=-√5*√5/2< -√5*√4/2=-√5. значит этот корень не подходит.
ответ: х(1)=(1-√17)/2, х(2)=(-1+√21)/2.
