В решении.
Объяснение:
Решить систему уравнений:
3х+2у=2
3х-2у=1 методом сложения
Смысл метода алгебраического сложения в том, чтобы при сложении уравнений одно неизвестное взаимно уничтожилось. То есть, чтобы коэффициенты при неизвестном каком-то были одинаковыми, но с противоположными знаками. Для того, чтобы этого добиться, преобразовывают уравнения, можно умножать обе части уравнения на одно и то же число, делить.
В данной системе ничего преобразовывать не нужно, коэффициенты при у одного значения и с противоположными знаками.
Складываем уравнения:
3х+3х+2у-2у=2+1
6х=3
х= 0,5
Теперь подставляем значение х в любое из двух уравнений системы и вычисляем у:
3х+2у=2
3*0,5+2у=2
2у=2-1,5
2у=0,5
у=0,25
Решение системы уравнений (0,5; 0,25).
Система уравнений имеет единственное решение, значит, графики данных уравнений пересекаются (координаты точки пересечения и являются решением системы уравнений).
Объяснение:
если известно, что искомая прямая y₁ = k₁x +b₁ параллельна прямой y=-4x+51 (у=кх +b), то мы знаем коэффициент k₁ = -4 при x, т.к. у параллельных прямых коэффициенты k и к₁ при х равны.
тогда мы уже имеем "половину" уравнения у₁ = -4х +b₁
теперь для определения b₁ используем то, что искомая прямая проходит через точку M(-1; 3). это означает, что координаты точки должны удовлетворять уравнению у₁ = -4х +b₁. подставим эти координаты
3= -4*(-1) +b₁ тогда b₁ = -1
и искомое уравнение
у₁ = -4х -1
теперь проверим, принадлежит ли построенному графику точка N(-50; 200). подставим ее координаты в уравнение у₁ = -4х -1
200 ≠ -4*(-50)-1
точка N(-50; 200) ∉ графику функции у₁ = -4х -1
тогда строим график по двум точкам
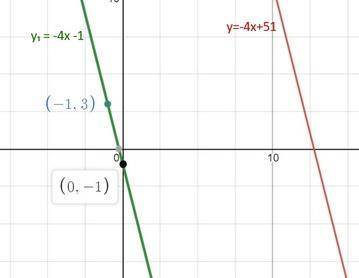
х = -1 у₁(-1) = 3 точка M(-1; 3)
х = 0 у₁(0) = -1
на первом фото построение по двум точкам у₁ = -4х -1 ║y=-4x+51
на втором показано, что точка N(-50; 200). ∉ графику у₁ = -4х -1