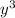куб числа по модулю 
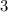(остатки от деления) сравнимы с 
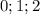соответственно когда 
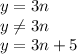, где 
. 
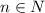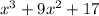
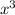так же как 
,
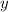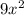дает остаток 
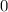, число 
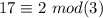, то есть остаток числа 
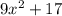равен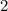 
при делений на .
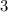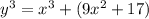
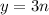слева остаток всегда равен 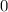, но справа уже не может поэтому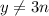 
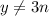, слева остаток при делений на 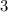как ранее был сказан равен 
, но тогда справа должно быть число дающее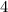 
, а оно дает при делений на 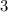остаток отсюда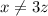 
подходит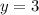 
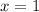
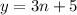, но оно так же не действительно , то есть решение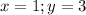 
В комментариях уточнения:
"Найдите при каких значениях х выполняется неравенство y≤2, функции y=√x"
x≥0; т.к. четный корень можно взять из не отрицательного числа.
y≤2;
√x≤2;
x≤4;
x ∈ [0;4];